2-7 统计指标:离散趋势
你好,我是悦创。
上节课我们学习了,集中趋势指标,并通过计算平均值、中位数、众数,了解了数据样本的一般水平。这节课,我们学习离散趋势指标,来了解一个数据的内部差异有多大。
什么是离散趋势指标
我以两支股票价格波动数据为例:
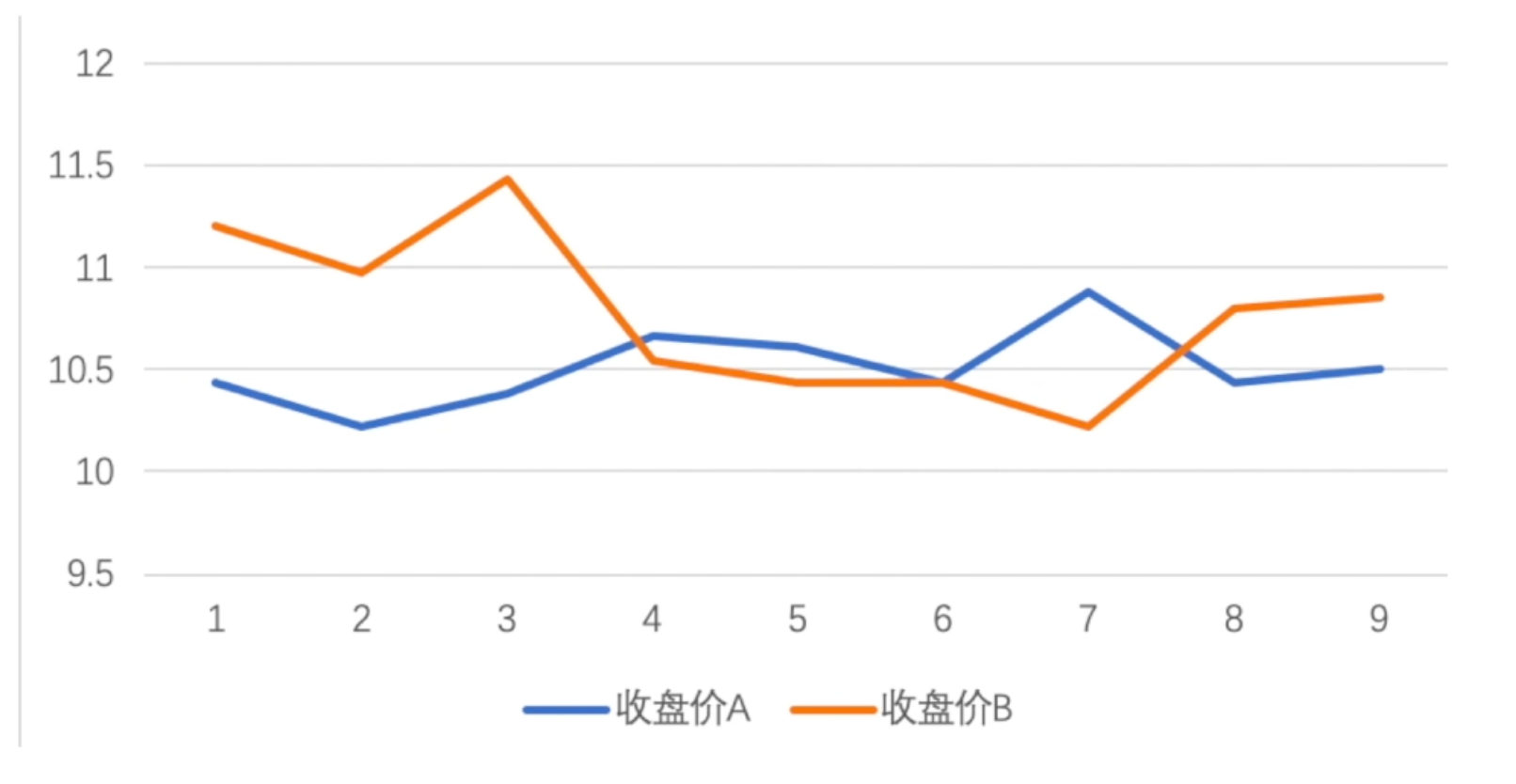
可以看到,股票 A,也就是蓝色这条线,它的波动比较平缓。股票 B 也就是橘色的那条,波动比较大。
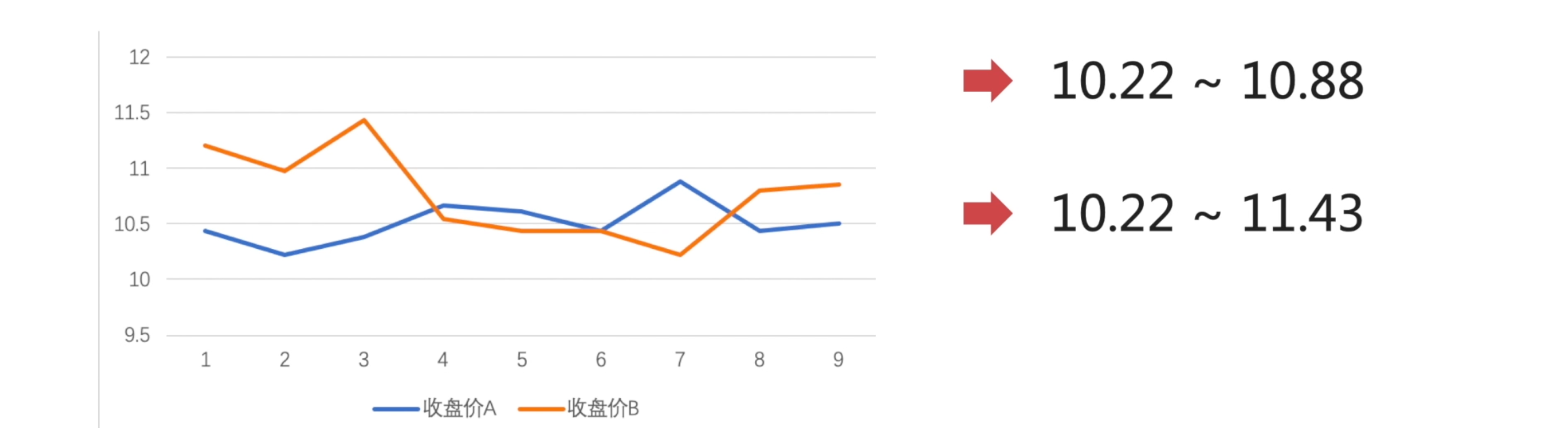
那用数值化来表示,股票 A 的波动幅度是在:10.22~10.88 之间;
股票 B 的波动幅度是在 10.22~11.43 之间。
通过图示,我们可以得出一个很简单的结论:股票 A 相对于股票 B——波动的幅度是更小的。「股票 B 比股票 A 更离散」
离散趋势指标,作为体现样本数据内部差异度的指标。 主要有三类指标可以表示:
- 极差
- 平均差
- 标准差
接下来,我们来看看这几个指标的具体概念和区别。
极差
我们将收盘价的数据,以折线图的形式进行表示:
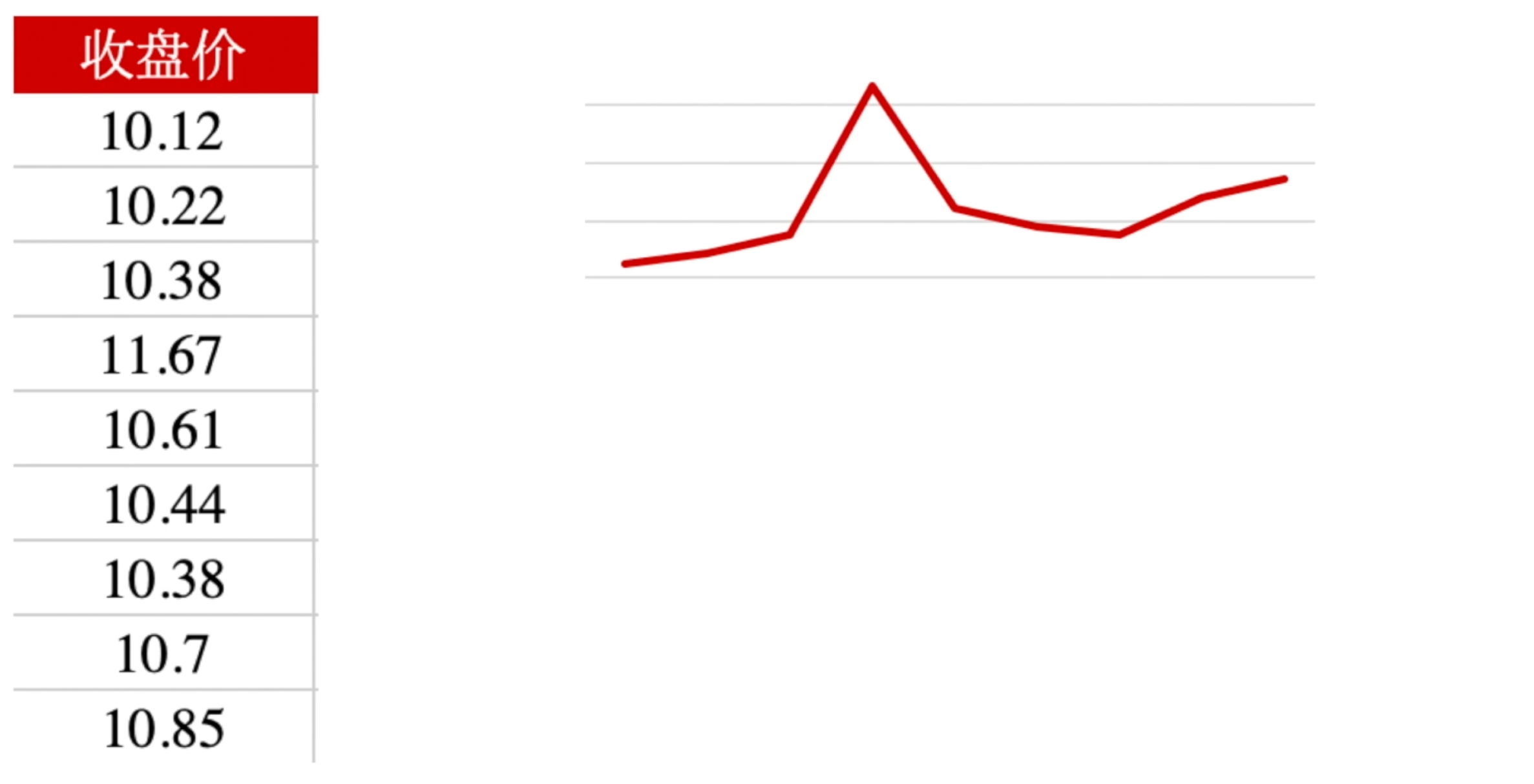
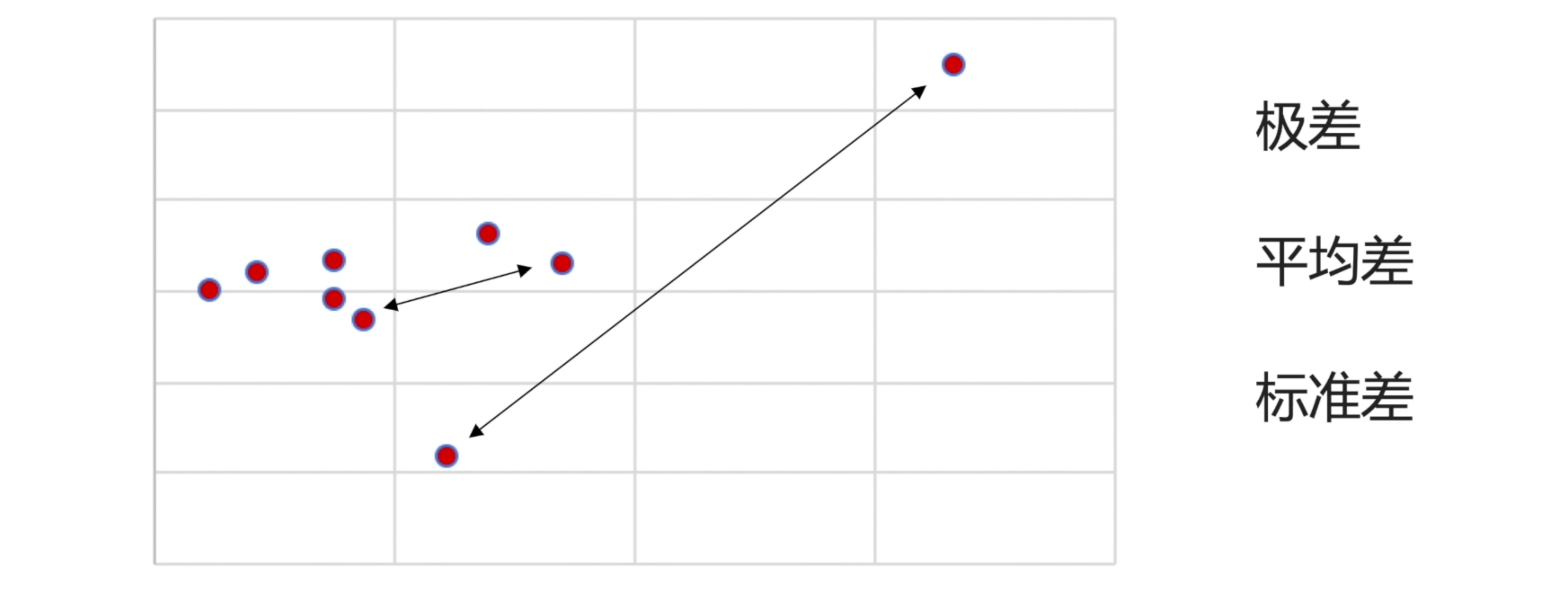
极差就是求:两个相差最远点的之间的距离。
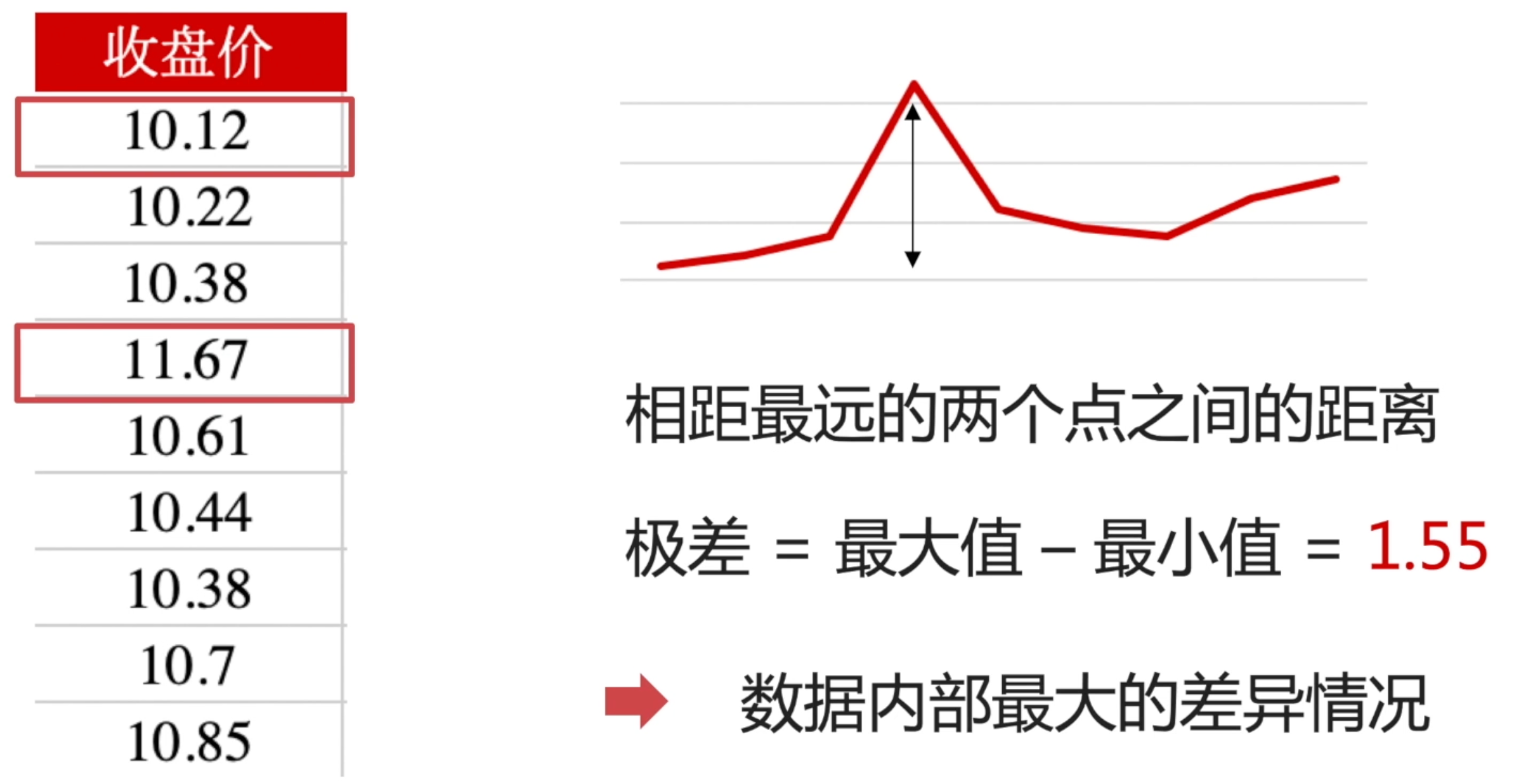
那在上面的收盘价中,最小的值是 10.12,最大的值是 11.67。那通过计算:极差=最大值-最小值=1.55 ,它体现的就是数据内部最大的差异情况。
那么极差大样本的数据,内部一定离散程度高吗?
我们来观察两组数据:

可以试想一下,上图左边是公司项目组 A 的业绩情况,右边是公司项目组 B 的业绩情况。
在项目组 A 中,表现最好与表现最差的,它们相差额度是 100万。
在项目组 B 中,表现最好与表现最差的,它们相差额度是 200万。
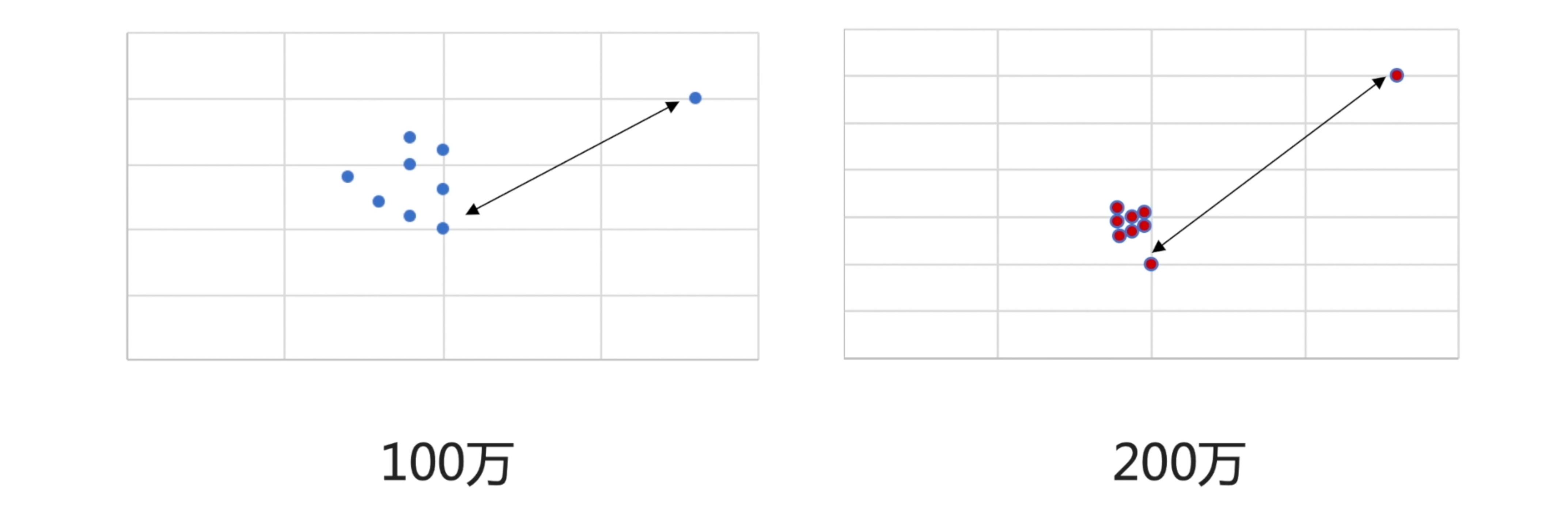
那么,通过观察我们的图表,项目组 A 相差 100 万,它们内部的离散程度,一定比项目组 B 相差 200 万极差的数据,离散程度要更小吗?——其实不一定的,也就是说: 极差不能体现,数据内部真正的离散程度 。那么想要知道一组数据内部真正的差异情况,我们可以使用平均差。
平均差
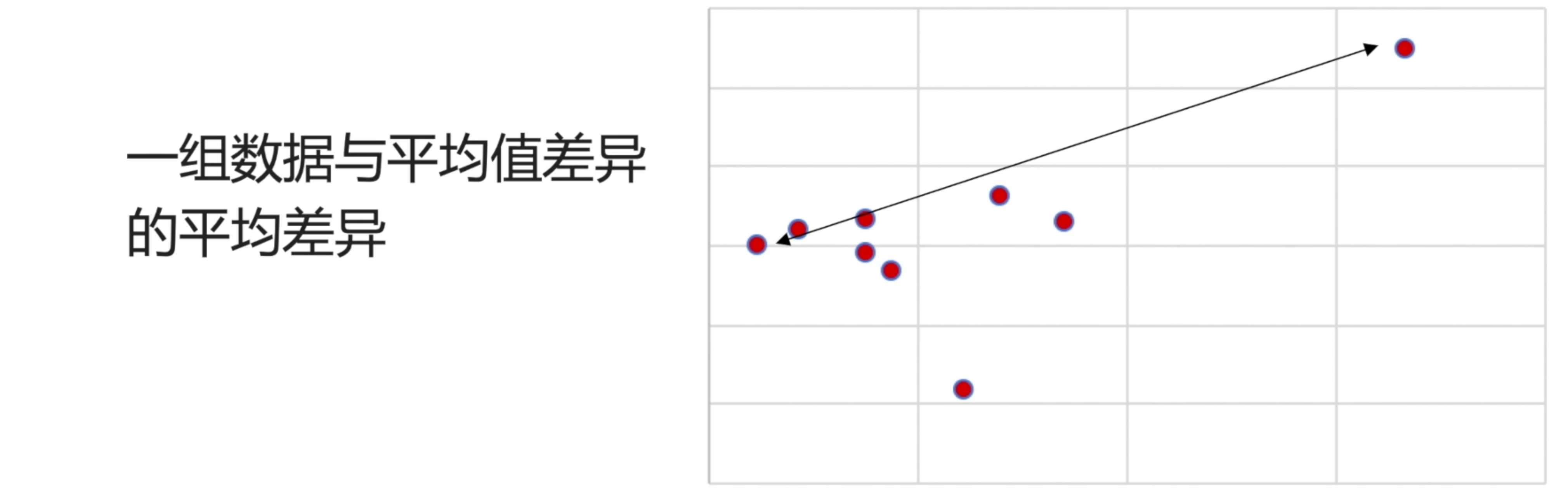
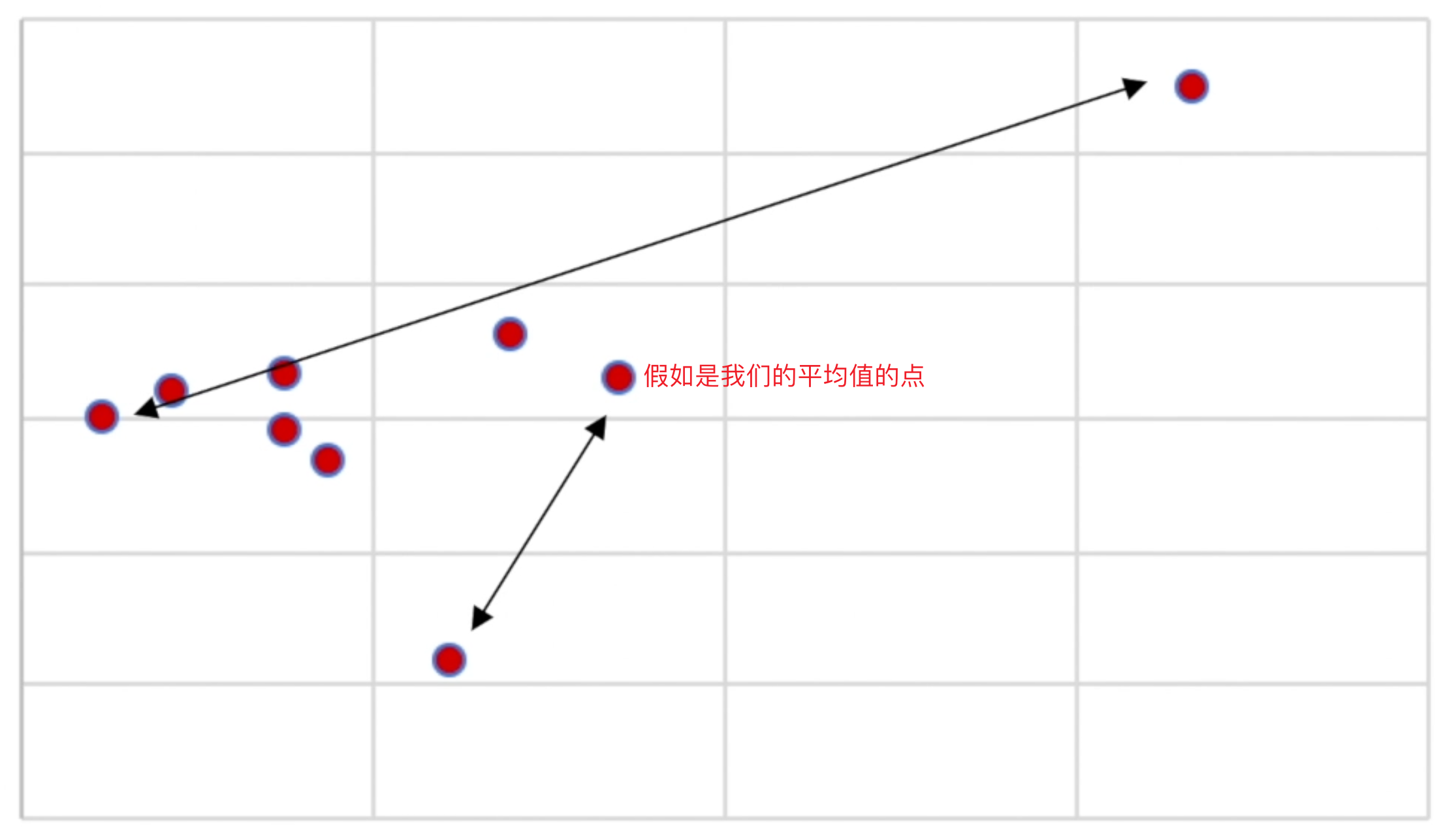
平均差,就是指:每一个点,每一个数据,它相对于我们的平均值,与平均值之间的平均距离——也就是点与点之间的平均差异程度,就是我们的平均差。
公式:

上面的 0.32 指的就是我内部的价格差异。
观察公式我们可以发现,我们 数据项个数 其实是不会变的,而分母的 |收盘价-均值| 差异越大,不就证明我这个公式的分母就越大。我这个平均差的指标就会越大,那数据内部的离散程度就越大。
这个时候,我们稍微的计算收盘价,头两天的交易差价,大概在 0.1 左右。头三天是在 0.26 = 10.38 - 10.12。
这几个值,你算起来都比 0.32 小的。那这个时候,你就要思考一下,是不是存在 异常值 导致这个平均差,比我们实际的真实情况要更大。
那为了,更好的观察到,我们每天收盘价的变化,我把涨跌幅也放进去。
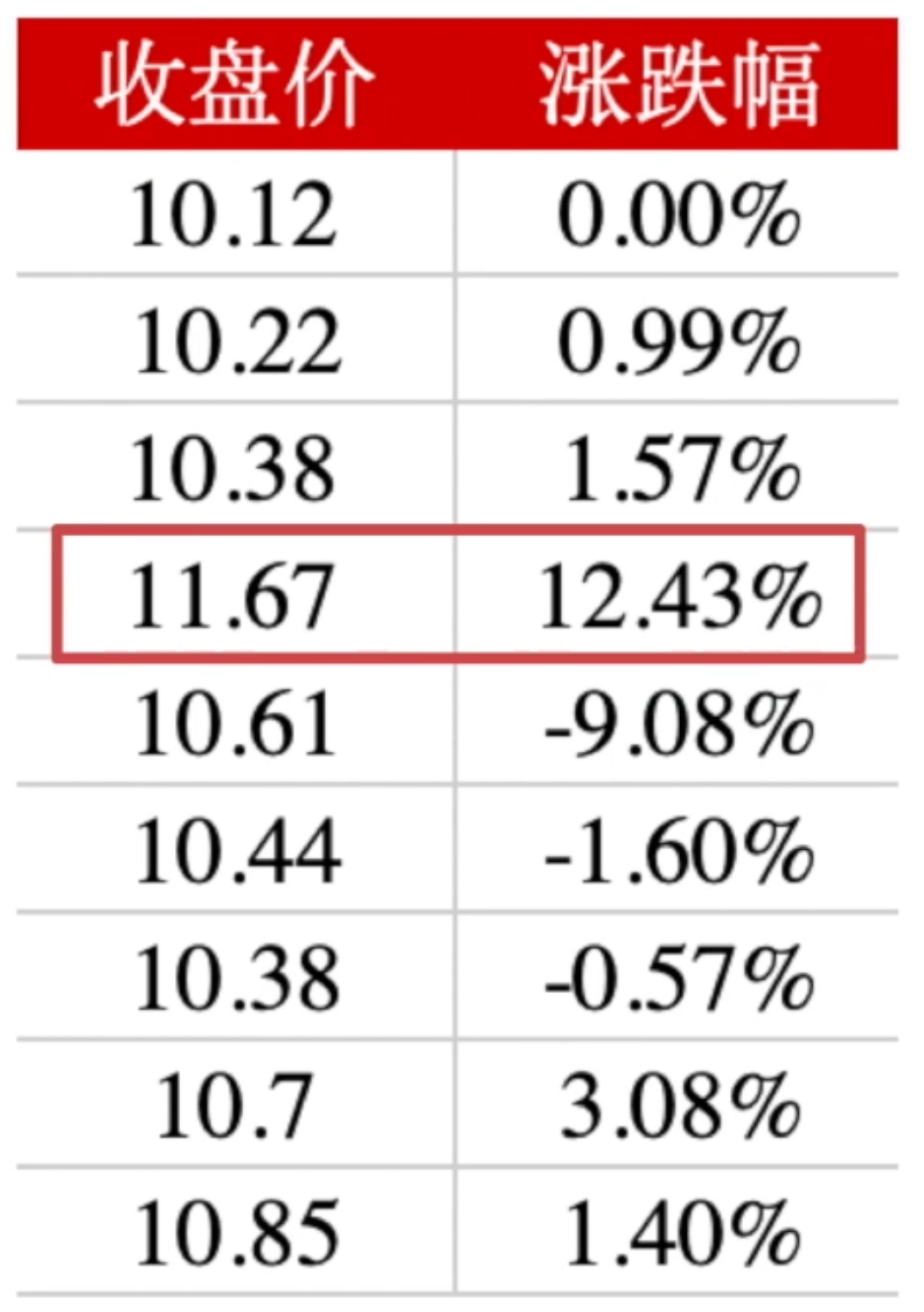
大家可以观察一下,它明显是一个异常值的数据。
那这个异常值,产生的原因有很多。
- 在股票市场中:可能是股东回购,导致这个市值上涨;或者是行业或者政策的利好;又或者是因为,供需失衡,导致市场对于这一家公司业务需求度上涨,然后导致股票的估值也上涨。当然还有其他原因。。。都会导致数据的异常。
- 但问题是:这种问题虽然是由事件驱动型,导致的异常数据,在样本量较小的时候,容易导致误差。但是!这个异常数据又是真实存在的数据,我们不能通过简单的刨除、或者使用其他数值来代替这个数据。
- 那这个时候,为了更好的去突出,对于离散程度,对于这种异常数据的敏感度,我们基于平均差,发展出了 标准差。
标准差
标准差的公式和平均差很相似:

相对于平均差,标准差更能够体现离散程度指标。说白了,更加放大了,它们之间的差异程度。
我们还是用刚刚的收盘股票数据,来验证一下。收盘价 A 是原有的收盘价数据,收盘价 B 是把异常值换成了和上一个交易日相同的数据。(也就是抹去了异常值的存在)
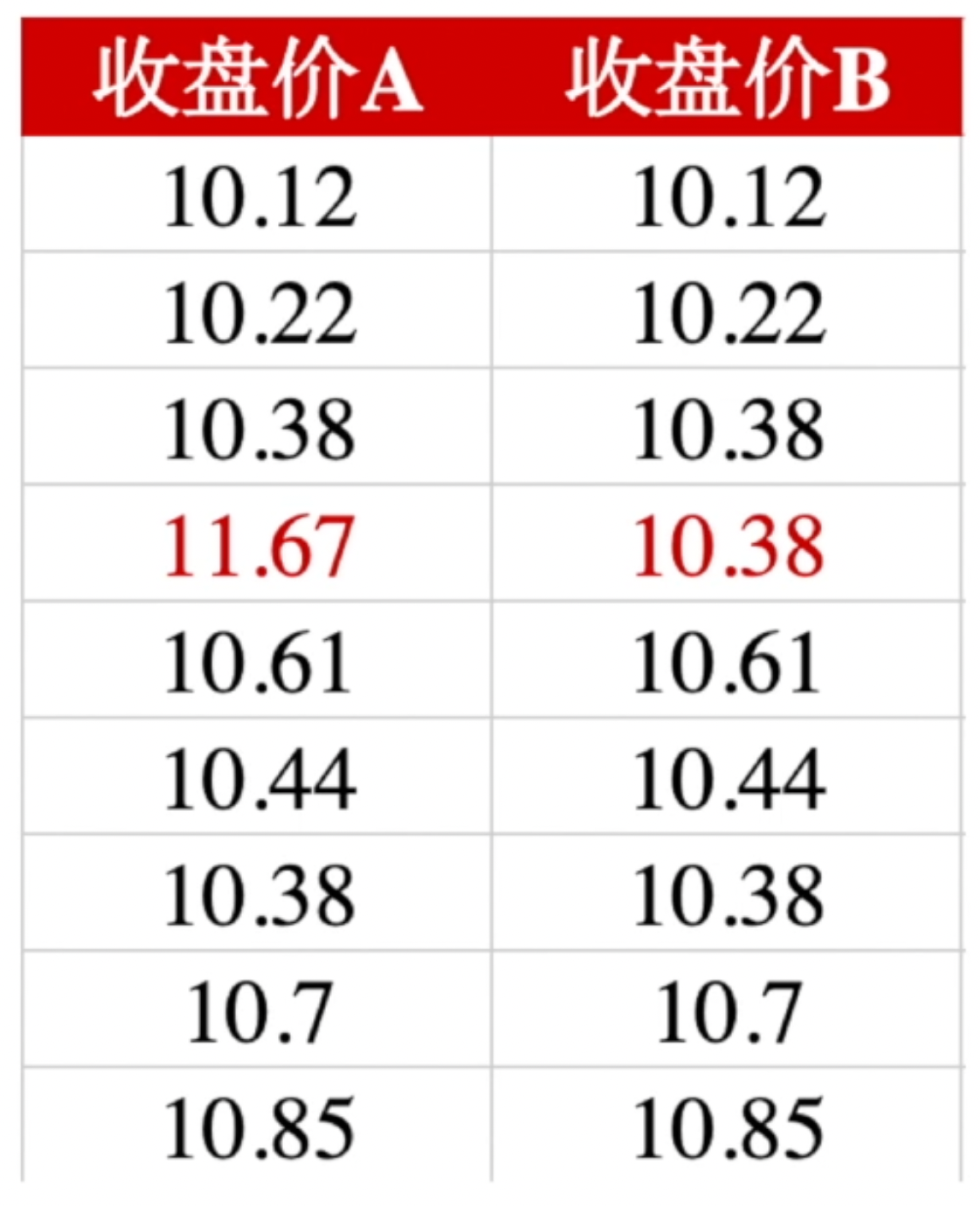
那这个时候,我们计算这两组数据的平均差和标准差。
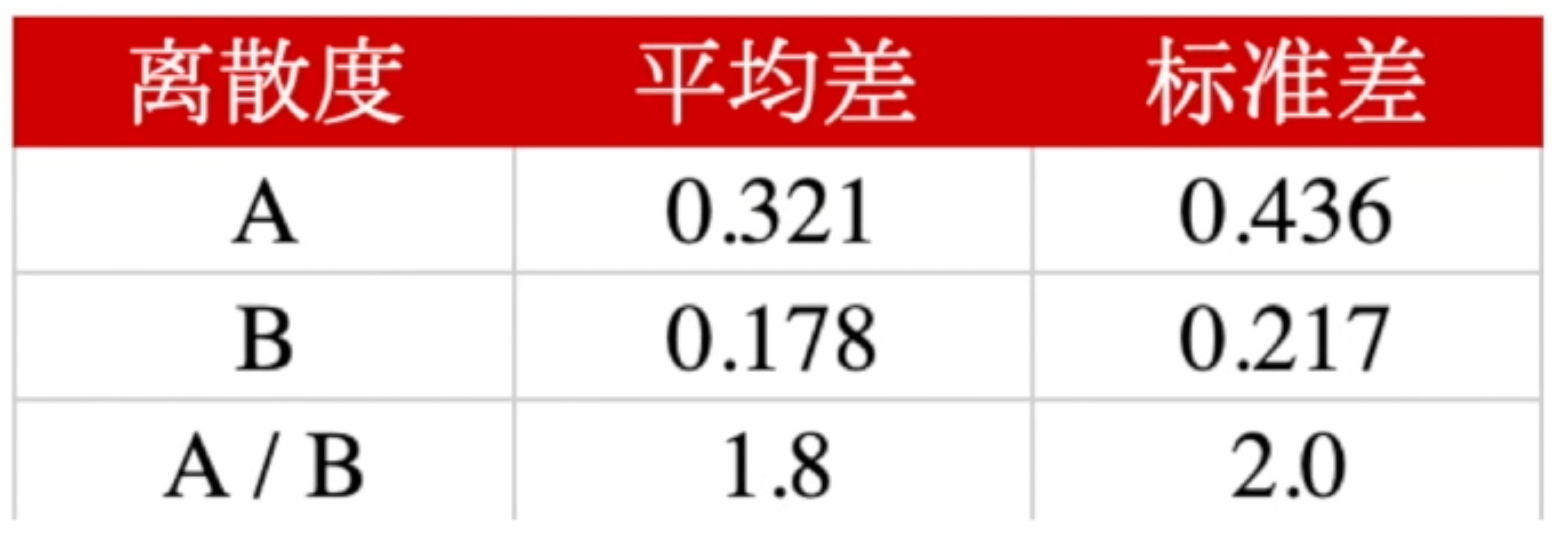
A/B 的平均差,差了 1.8 倍。标准差差了 2.0 倍。也就是说用标准差更能「更直观」体现数据内部的差异程度。「离散程度」
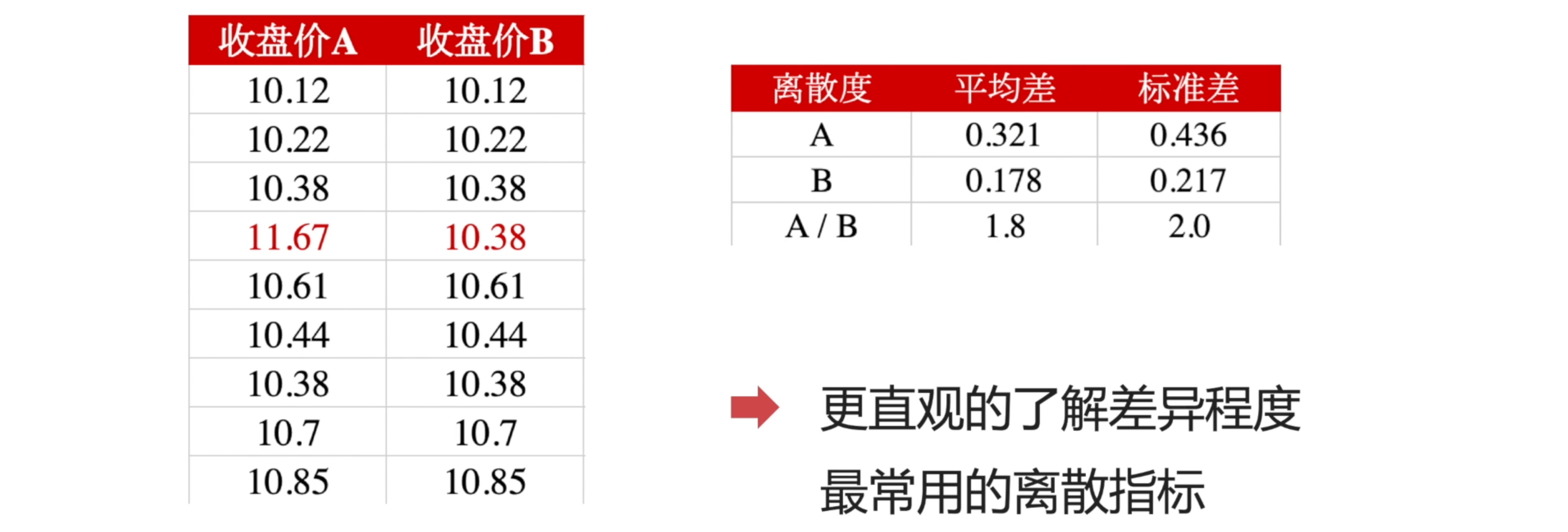
实际上,标准差也是我们最常用的离散指标。在风控相关的:比如股票投资品类的风险的时候,我们都是使用标准差来对价格数据进行计算。
标准差越大的,风险也就会越大。因为,它的波动幅度越大。
章节回顾
课后作业

期待你和我一起,用数据解析世界
欢迎关注我公众号:AI悦创,有更多更好玩的等你发现!
公众号:AI悦创【二维码】

AI悦创·编程一对一
AI悦创·推出辅导班啦,包括「Python 语言辅导班、C++ 辅导班、java 辅导班、算法/数据结构辅导班、少儿编程、pygame 游戏开发」,全部都是一对一教学:一对一辅导 + 一对一答疑 + 布置作业 + 项目实践等。当然,还有线下线上摄影课程、Photoshop、Premiere 一对一教学、QQ、微信在线,随时响应!微信:Jiabcdefh
C++ 信息奥赛题解,长期更新!长期招收一对一中小学信息奥赛集训,莆田、厦门地区有机会线下上门,其他地区线上。微信:Jiabcdefh
方法一:QQ
方法二:微信:Jiabcdefh

更新日志
1c35a-于aed17-于cbb3a-于610fe-于76989-于86c50-于027da-于