决策树算法
1. 决策树算法概述
你好,我是悦创。
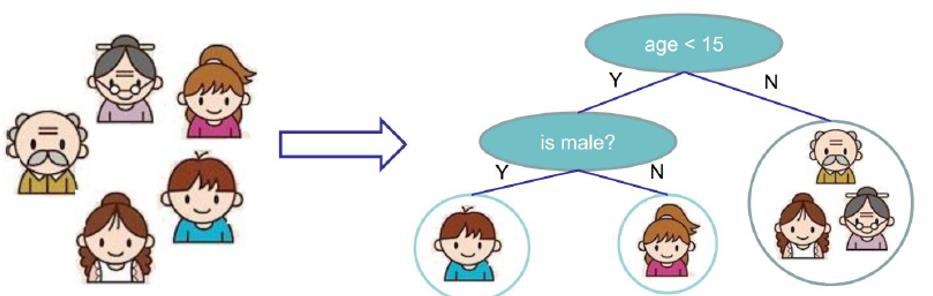
家里有五口人,爷爷奶奶、两个孩子、一个母亲。
我们要做个分类,在分类中,我们要做个判断:谁爱玩电脑游戏。
谁爱玩电脑游戏肯定是数据当中这些特征所决定的吧,假如当前数据中有两个特征:年龄、性别。这两个特征都会对结果产生影响。上图是我们现在构建出决策树的模型。
从数据栏当中,回落到第一个判断的键当中。
从上往下走,通过对年龄的判断,年龄是不是小于 15 岁,如果年龄小于 15岁,他是潜在有玩游戏的可能性的。那就让他往左边走:
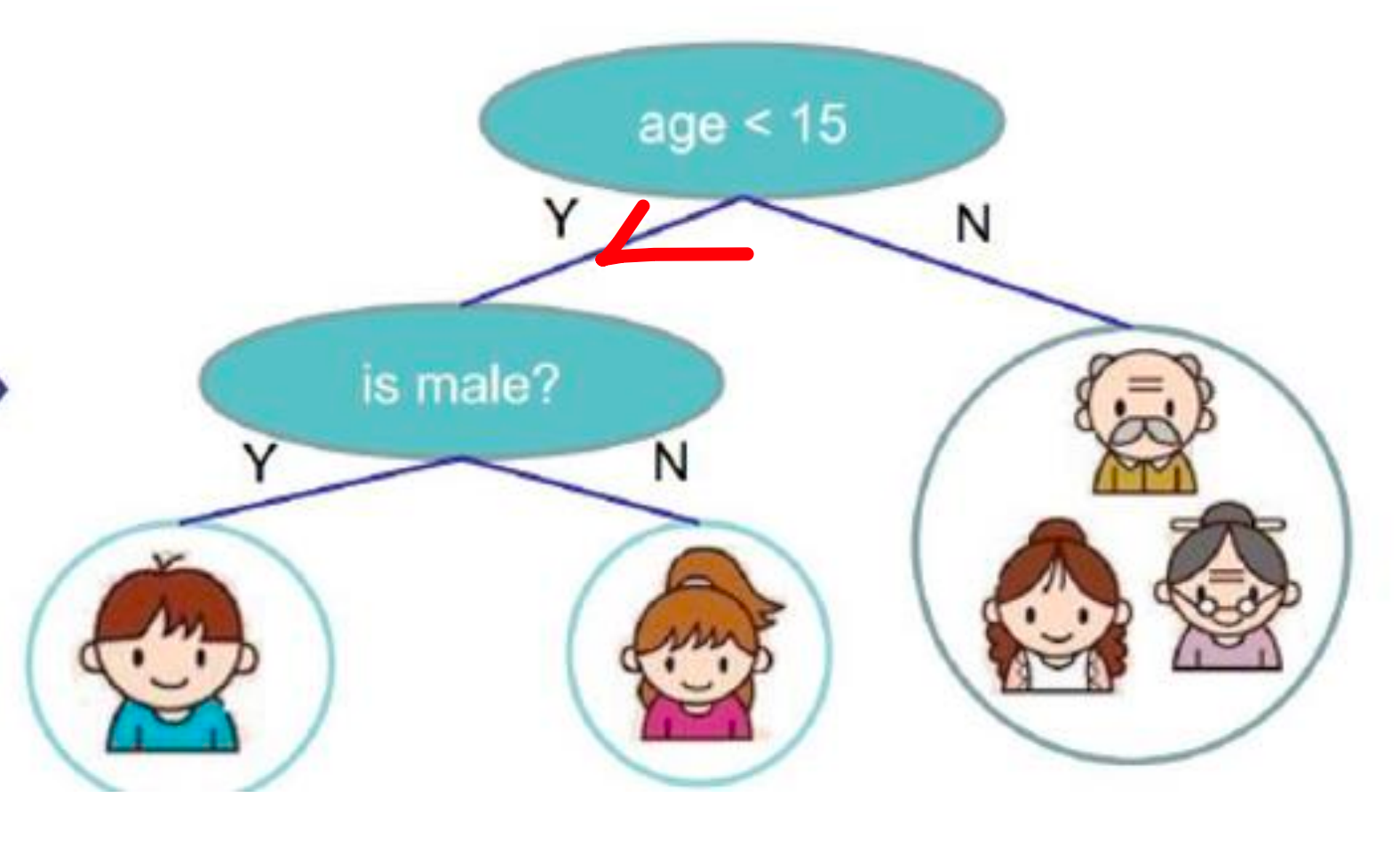
如果不是小于 15岁的,我们就把他排除在外了,认为他是不喜欢玩电脑游戏的。
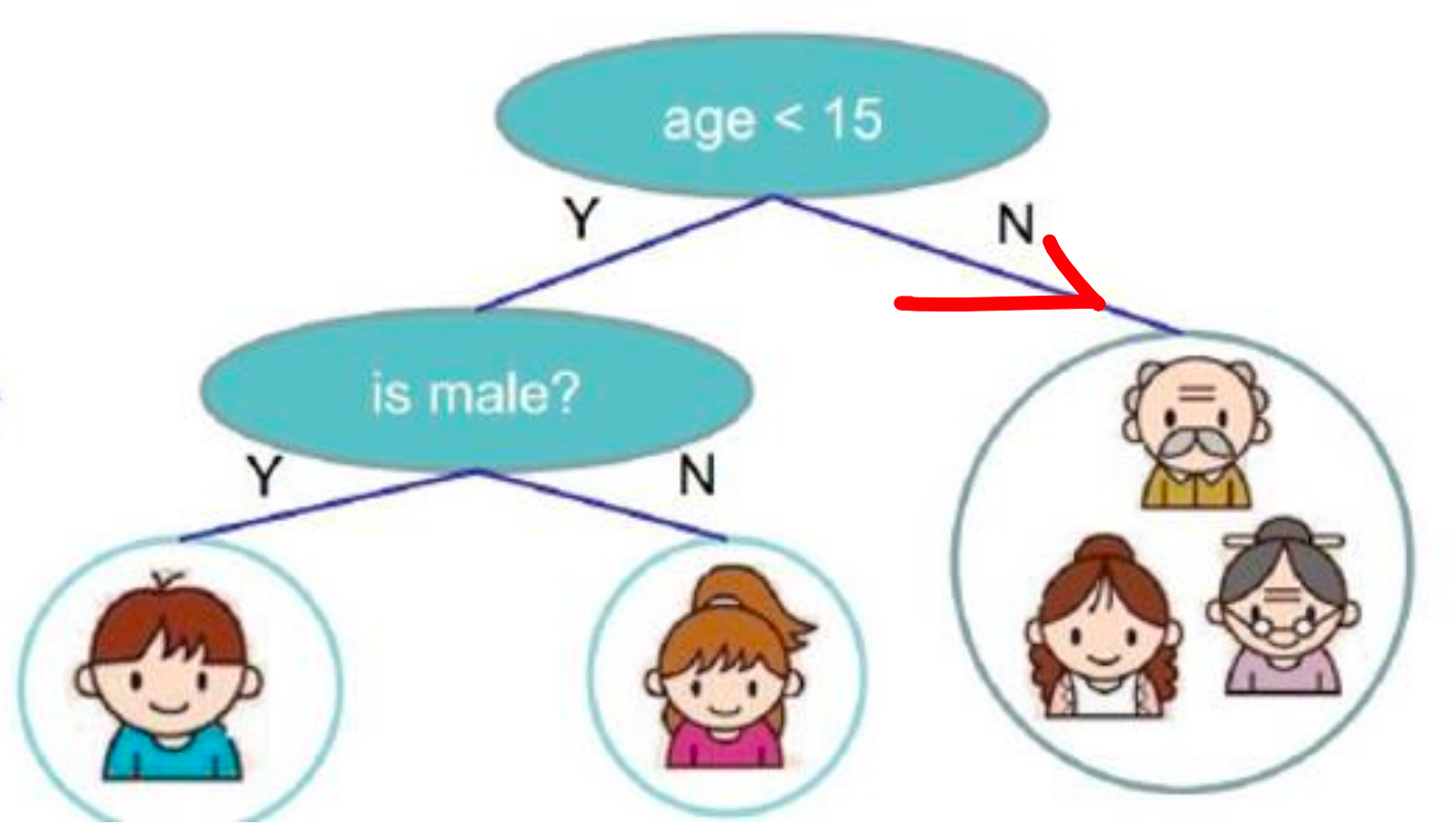
所以,我们第一步通过这个年龄的判断,有些喜欢玩有些不喜欢玩。那现在,不喜欢玩的,相当于到这里就截止了。
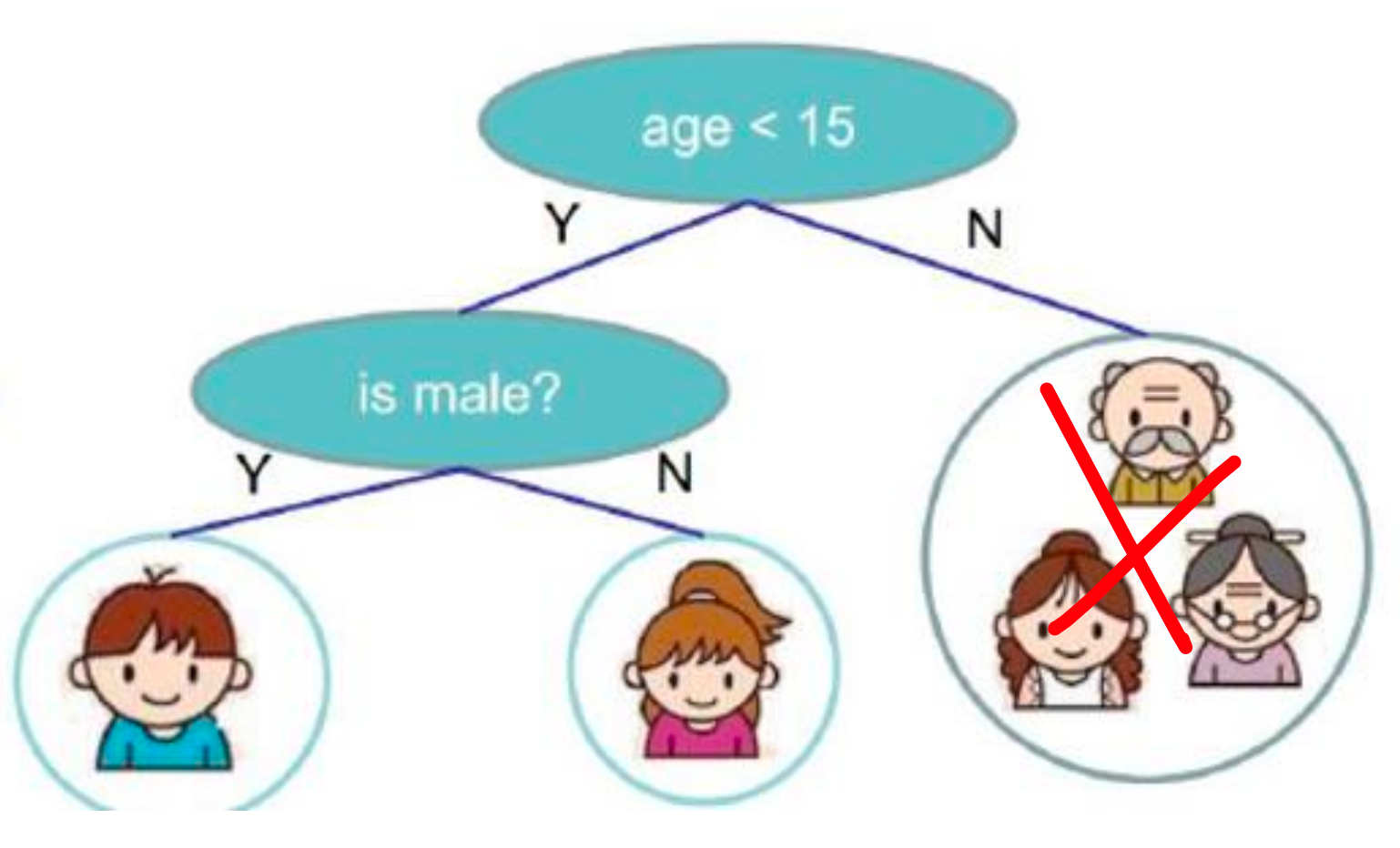
那左边我们继续,我们不光对他的年龄做了一个判断,接下来我们对他的性别再做了一次判断。如果,是一个男孩的话,他是喜欢玩游戏的。如果她是女孩是不喜欢玩游戏的。
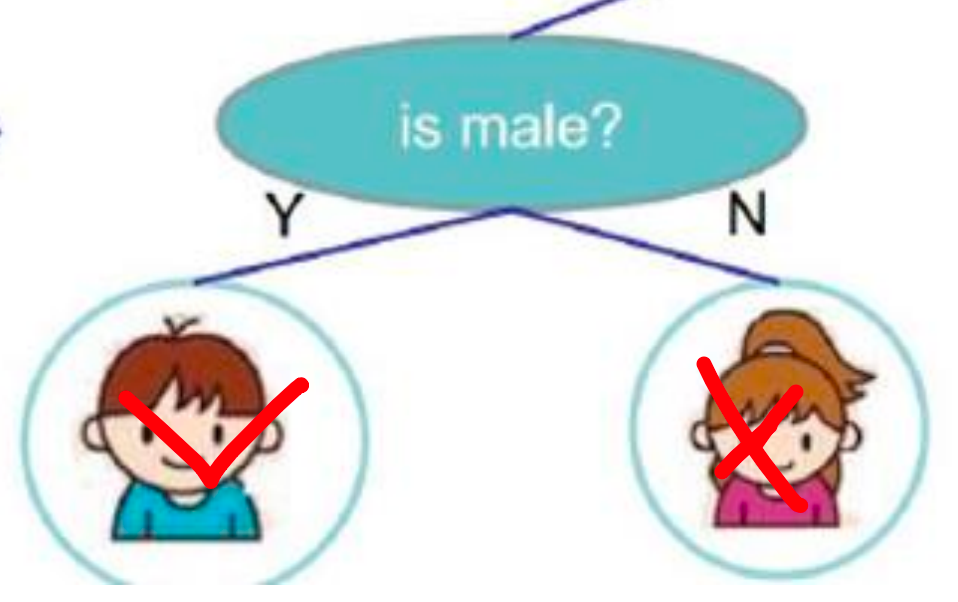
上面所描述的就是决策,解决问题的基本流程。看起来是不是比较简单呢?
那大家想一下:当大家看到上面的决策树的时候,大家能不能想到什么问题呢?或者说这里有没有一些东西,值得我们思考一下。
回想一下,左边是样本,右边是我们的判断树,我们先判断了年龄,看是不是小于 15、又判断了性别,是男孩还是女孩。那此时大家肯定会问一个问题:我能不能先判断性别,再判断年龄。在这个项目中好像也是的,也是可以的。
反正这个小男孩,是男性且必须小于 15 岁。——那先判断哪一个应该都可以吧,应该没有什么区别吧。
但是, 在决策树中,不是这样的。决策树把前后顺序把控的特别严格。一旦你把前后顺序改变,最后的结果,一定会发生一些变化的。
1.1 树模型
决策树:从根节点开始一步步走到叶子节点(决策)
所有的数据最终都会落到叶子节点,既可以做分类也可以做回归
那我们来想想,为什么把年龄放在第一个,性别放在下一个呢?你说,我们要做一个分类任务。然后这个分类任务要分两次去做。所以,我们都希望在第一次做的时候,尽可能都做对了。第二次做的时候,再做一个微调,再做一个细致一些的划分。 「第一次过滤的时候,过滤大部分的数据,第二次过滤的时候过滤一些细致性的东西」
所以说,在决策树当中,也是遵循这个点。
我们把起始的特征,叫做:根节点。这个区分比较强的,把它放在最前面。「它可以进行大致的判断」
那下面,老二来了。它虽然没有根节点强,但也能起到划分的作用。「细化」——那你说老大和老二能替换吗?一个首发阵容、一个替补整容。能替换么?
先上场哪个,肯定先上首发是不。不能上替补吧~
所以说,我们先放哪个节点,就是哪个比较厉害的,把结果分的比较厉害。接下来再上替补,进行细致的划分。
那你会问:凭什么 age 是首发,sex 是替补?
我给你讲的决策树的模型,就是为了解决这一的问题。
决策树可以做分类回归。
1.2 树组成
根节点:第一个选择点
非叶子节点与分支:中间过程
叶子节点:最终的决策结果
1.3 决策树的训练与测试
训练阶段:从给定的训练集构造出来一棵树(从跟节点开始选择特征,如何进行特征切分)「核心」
测试阶段:根据构造出来的树模型从上到下去走一遍就好了「有数据,得到结果」
一旦构造好了决策树,那么分类或者预测任务就很简单了,只需要走一遍就可以了,那么难点就在于如何构造出来一颗树,这就没那么容易了,需要考虑的问题还有很多的!「也就是比如上面的例子,为什么是小于 15岁,18岁可不可以?19岁呢?」也就是这些数据才是最难的。
2. 熵的作用
那接下来我们来说决策树中最核心的一点:怎样选特征!(我为什么选择年龄作为根节点?为什么选择 15岁呢?)这个就是我们现在的问题,这个问题很重要。
2.1 如何切分特征(选择节点)
问题:根节点的选择该用哪个特征呢?接下来呢?如何切分呢?
想象一下:我们的目标应该是根节点就像一个老大似的能更好的切分数据(分类的效果更好),根节点下面的节点自然就是二当家了。
目标:通过一种衡量标准,来计算通过不同特征进行分支选择后的分类情况,找出来最好的那个当成根节点,以此类推。
比如你数据集中有十个特征:年龄、性别、xxxxxxx
那用哪个呀?——肯定选择分类效果最强的特征。当做大当家。
大当家好了之后,来二当家。以此类推。。。。。。
那我,怎么选择出大当家呢?
需要一种判断方法,找到一个标准!以数据说话。
2.2 衡量标准-熵
- 熵:熵是表示随机变量不确定性的度量(解释:说白了就是物体内部的混乱程度,比如杂货市场里面什么都有那肯定混乱呀,专卖店里面只卖一个牌子的那就稳定多啦)
按我的来说就是:混乱程度 ,你现在到了义乌小杂货市场。这不是有两元店、十元店、卖包、卖鞋的都有。那你说你到两元店里面,里面一百多个商品。你买某一个商品的可能性——高还是低呢?
里面一百多个商品,你就偏偏买扑克牌,那你选中扑克牌的可能性是高还是低?——显然是比较低的吧。——为什么?
因为,它里面可选的东西太多了。杂七杂八的杂货市场,啥都有。你买其中的随便一个东西,概率都很低的。
那你说:杂货市场,混不混乱。显然是混乱的。——你到两元店里面,买啥都不确定。越混乱的地方,不确定的度量就高呀~此时,你的墒值就 大 。
那什么时候墒值小呢?
你想在要买手机,到了苹果专卖店,说:我想买部华为手机,人家是不是得打你呀。——你到苹果专卖店,是不是只能买到苹果手机,那你说你有什么不确定性呢?你已经非常确定了,你只能买苹果手机。所以说,此时的不确定性度量非常小。那墒值就小吧。
上面就简单的跟你说墒值什么时候大,什么时候小。
那熵值什么时候大、什么时候小,跟我们决策树有什么关系?
举个例子:
我现在有两个类别:
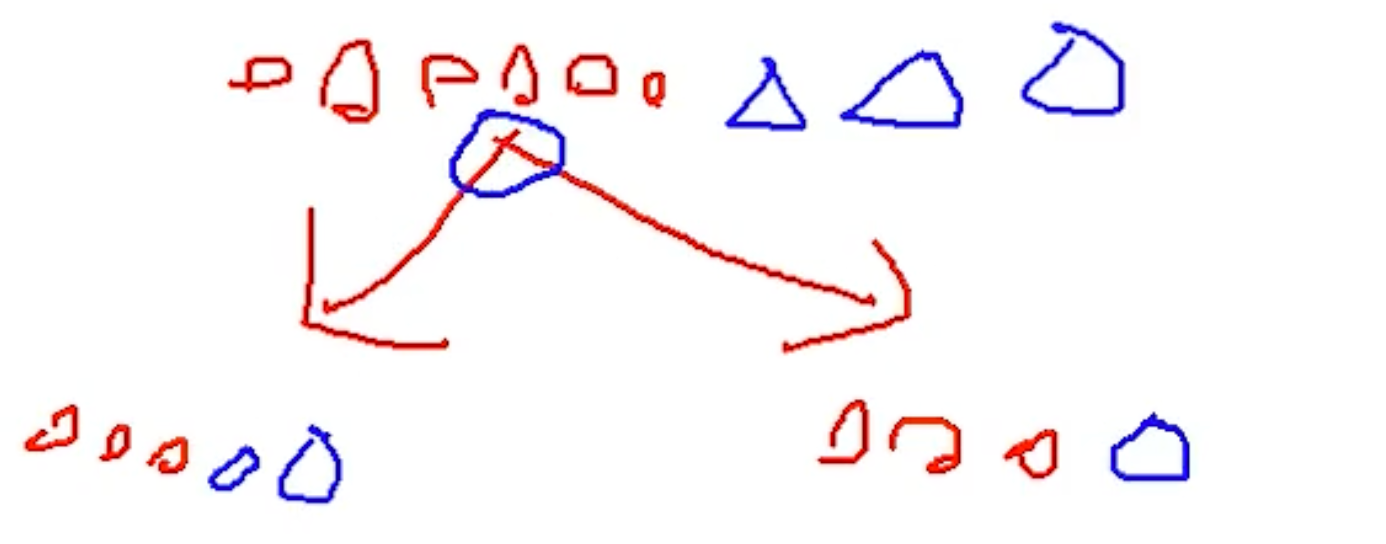
那从上面的结果来看,分不分的开?——显然是分不开的。那比如现在 100 个类别,那左边的混进去 100 个类别,那左边的熵值就比较的大。那我再画另外一种:

那现在上面为 A 方案,下面为 B 方案,你说哪个方案好?——肯定 B 方案好吧,B 方案后,为的左子树和右子树都是比较纯的吧。都是自己家人,圆圈都放一起了。数据也比较纯了。
这就是我们分类的一个标准,咱们要找到一个衡量标准,也就是分类效果的好坏。怎么评估呢?看分类完,经过一次决策完之后,咱们熵值的大小。
接下来,我们来看公式。
- 公式:

pi 概率值
取到红色的概率:75%;
取到蓝色的概率:25%;
经过决策之后的,概率值。
对数 logpi
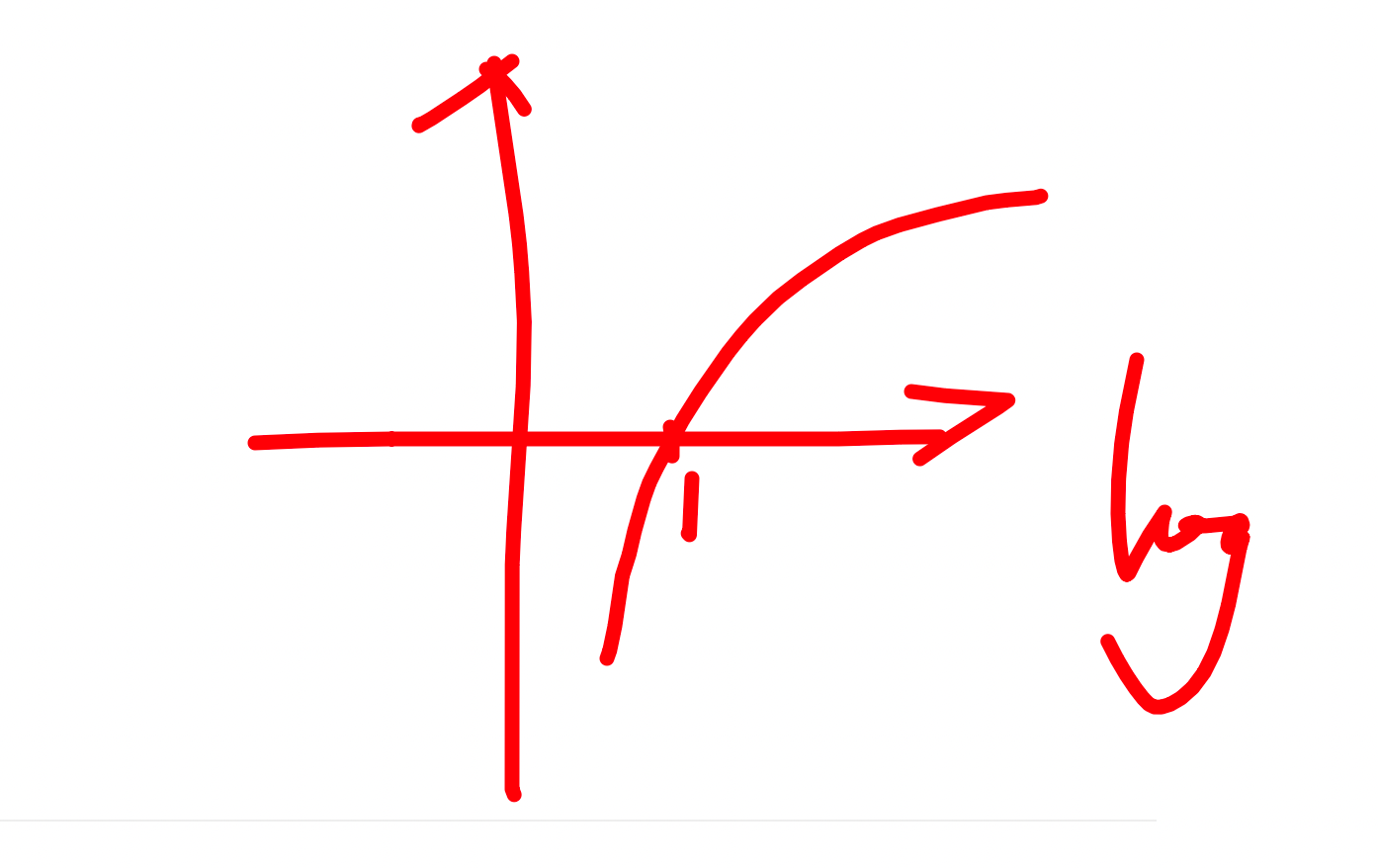
概率的取值范围呢:0<=pi<=1,对数函数在 0~1 之间都是负数,所以在前面公式我添加了一个负号。整个对数函数等于向上反转了。
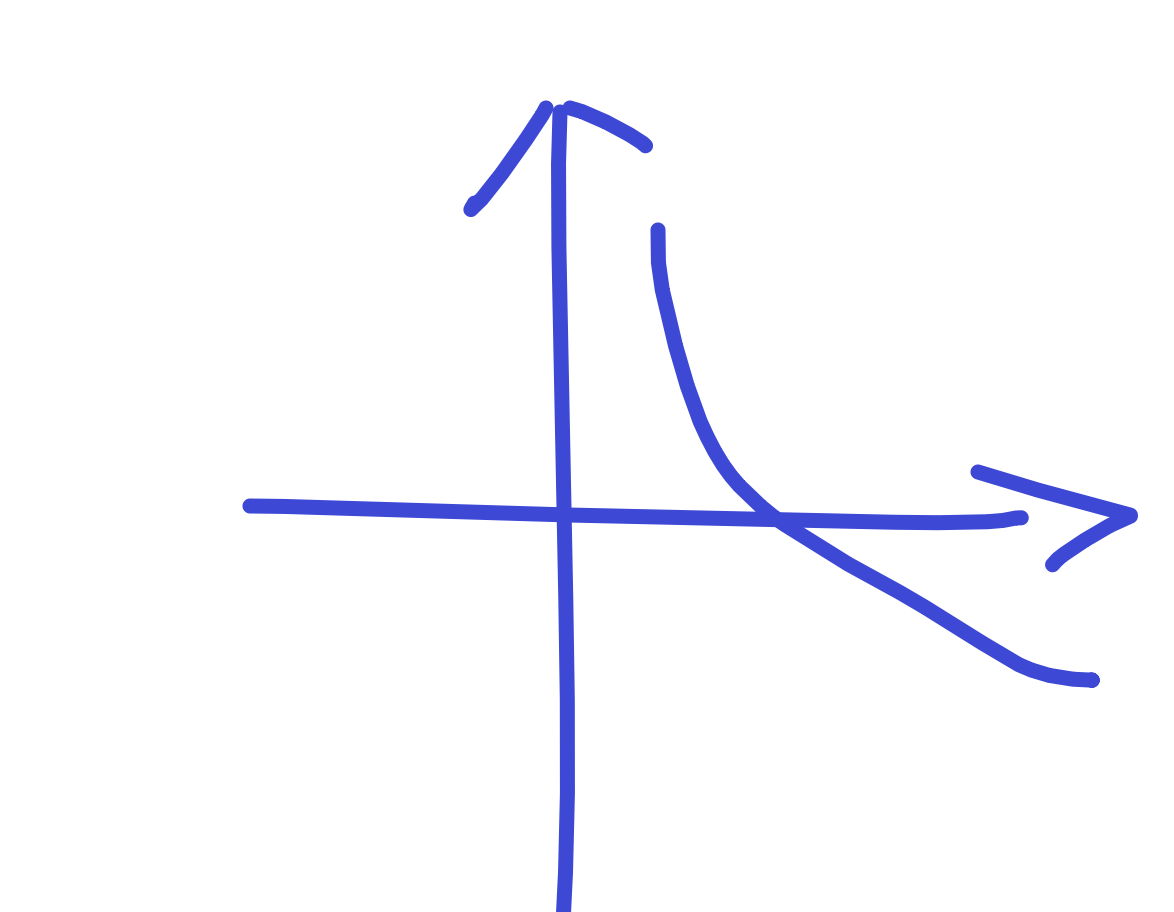
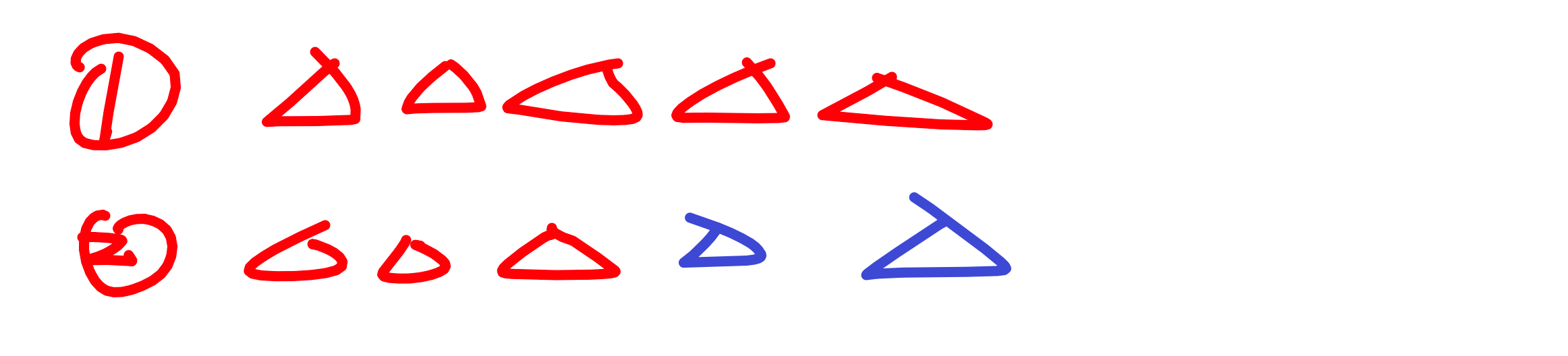
现在有 1、2 分类结果,那现在对于我们的 1 类来说,是不是取到的概率是 100% 呢。
对于 2 类来说,取到红色:60%,取到蓝色 40%。——那你想一下,你希望概率大好还是概率小好呢?
概率越高,从上图可知,纯度越高。所以说,当我们计算得到的概率值接近 1 的时候,才是我们想要的。这样你就发现,概率越高,熵值越小「看图就知道」概率值越低的时候,得到的熵值就越大。
= 对于每一个类别都进行计算并相加在一起,这就是我们熵值最终的结果了。
一个例子
A 集合 [1, 1, 1, 1, 1, 1, 1, 1, 2, 2]
B 集合 [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
一共有 10个。
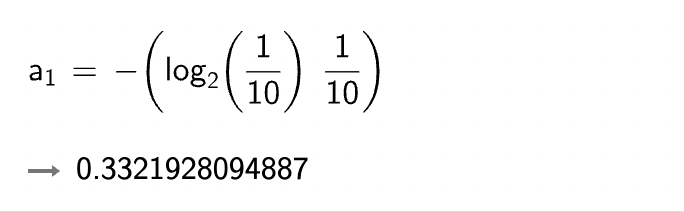
=>
= 0.3321928094887 * 10
= 3.321928094887
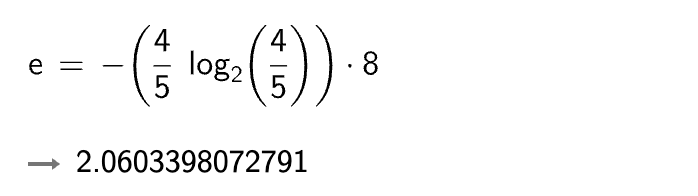
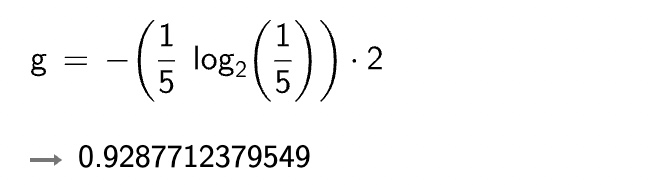
r = H(A1) + H(A2)
显然 A 集合的熵值要低,因为 A 里面只有两种类别,相对稳定一些。而。B 中类别太多了,熵值就会大很多。(在分类任务中我们希望通过节点分支后数据类别的熵值大还是小呢?)
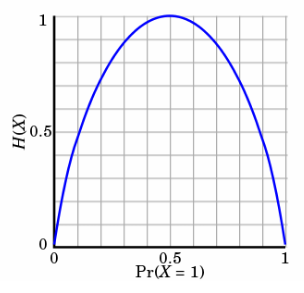
- 熵:不确定性越大,得到的熵值也就越大
- 当 p=0 或 p=1 时,H(p)=0 ,随机变量完全没有不确定性
- 当 p=0.5 时,H(p)=1 ,此时随机变量的不确定性最大
如何决策一个节点的选择呢?
信息增益: 表示特征 X 使得类Y的不确定性减少的程度。(分类后的专一性,希望分类后的结果是同类在一起)
「数据混在一起的时候熵值,数据分类后,比如分类了左右节点。那我既可以算左边的熵值,也可以算右边的熵值。是不是可以左右加在一起,小于原本的熵值,那是不是进步了。不管进步多少,进步了就行。『信息增益也就是使用熵值作为衡量标准。』
3. 决策树构造实例
3.1 数据&需求
| ID「序号」 | outlook「」天气 | temperature「」天气怎么样 | humidity「」湿度 | windy「」有无风 | play「」有没有去打球 |
|---|---|---|---|---|---|
| 1 | sunny | hot | high | FALSE | no |
| 2 | sunny | hot | high | TRUE | no |
| 3 | overcast | hot | high | FALSE | yes |
| 4 | rainy | mild | high | FALSE | yes |
| 5 | rainy | cool | normal | FALSE | yes |
| 6 | rainy | cool | normal | TRUE | no |
| 7 | overcast | cool | normal | TRUE | yes |
| 8 | sunny | mild | high | FALSE | no |
| 9 | sunny | cool | normal | FALSE | yes |
| 10 | rainy | mild | normal | FALSE | yes |
| 11 | sunny | mild | normal | TRUE | yes |
| 12 | overcast | mild | high | TRUE | yes |
| 13 | overcast | hot | normal | FALSE | yes |
| 14 | rainy | mild | high | TRUE | no |
- 数据:14 天打球情况
- 特征:4 种环境变化
- 目标:构造决策树
3.2 步骤
- 划分方式:4种
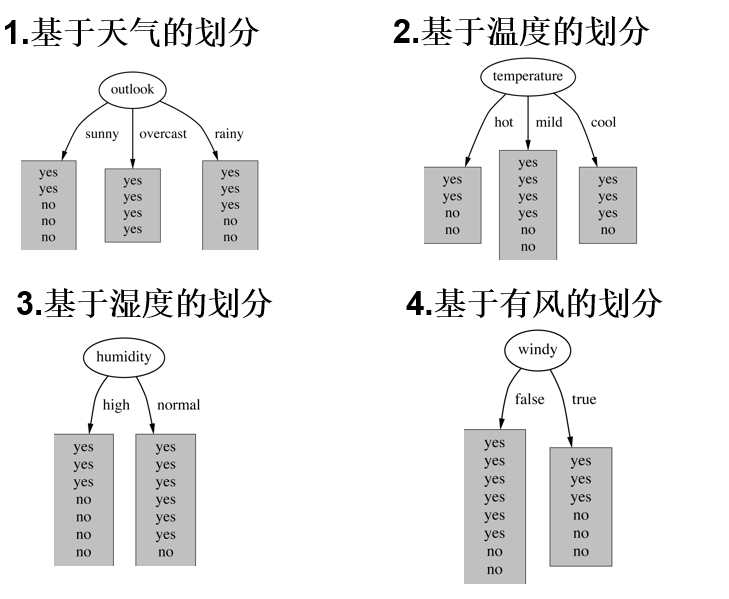
- 问题:谁当根节点呢?
- 依据:信息增益「哪个信息增益大,也就是哪个熵值下降大,我们就把哪个当作根节点」=分类完-之前熵值
3.2 原始数据熵值
在确定根节点之前,我们把原始数据的熵值计算出来。历史的熵值肯定是看 play,也就是结果。
- no: 5
- yes: 9
在历史数据中(14天)有 9 天打球,5 天不打球,所以此时的熵应为:
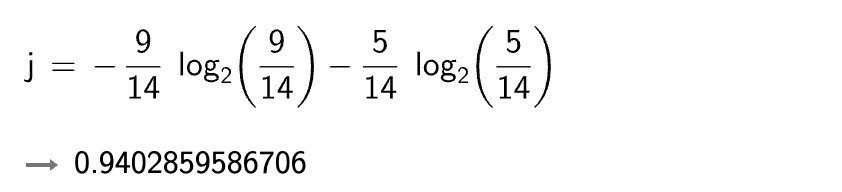
- 4 个特征逐一分析,先从 outlook 特征开始:
Outlook = sunny 时,熵值为 0.971
Outlook = overcast 时,熵值为 0
Outlook = rainy 时,熵值为 0.971
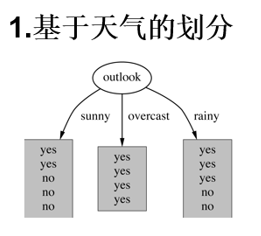
算完结果之后,我们可以直接加么?显然是不行的。为什么?因为它们三个「sunny、overcast、rainy」是不一样的吧。
我们需要做一个加权:概率「权值」*熵值
- 根据数据统计,outlook 取值分别为 sunny,overcast,rainy 的概率分别为:5/14, 4/14, 5/14
- 熵值计算:5/14 * 0.971 + 4/14 * 0 + 5/14 * 0.971 = 0.693
- (gain(temperature)=0.029 gain(humidity)=0.152 gain(windy)=0.048)
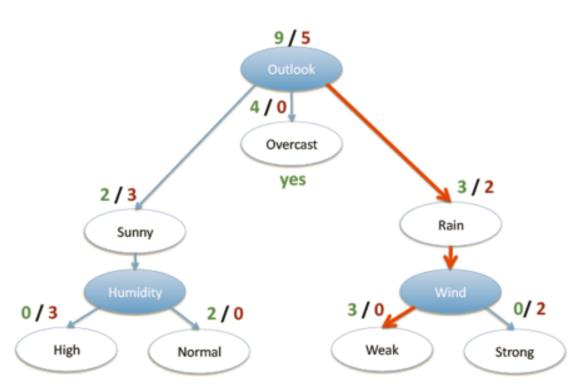
- 信息增益:系统的熵值从原始的 0.940 下降到了 0.693,增益为 0.247
- 同样的方式可以计算出其他特征的信息增益,那么我们选择最大的那个就可以啦,相当于是遍历了一遍特征,找出来了大当家,然后再其余的中继续通过信息增益找二当家!
4. 信息增益率与 gini 系数
4.1 ID3:信息增益(有什么问题呢?)
ID3:信息增益(有什么问题呢?)
C4.5:信息增益率(解决 ID3 问题,考虑自身熵)
CART:使用 GINI 系数来当做衡量标准
GINI系数:
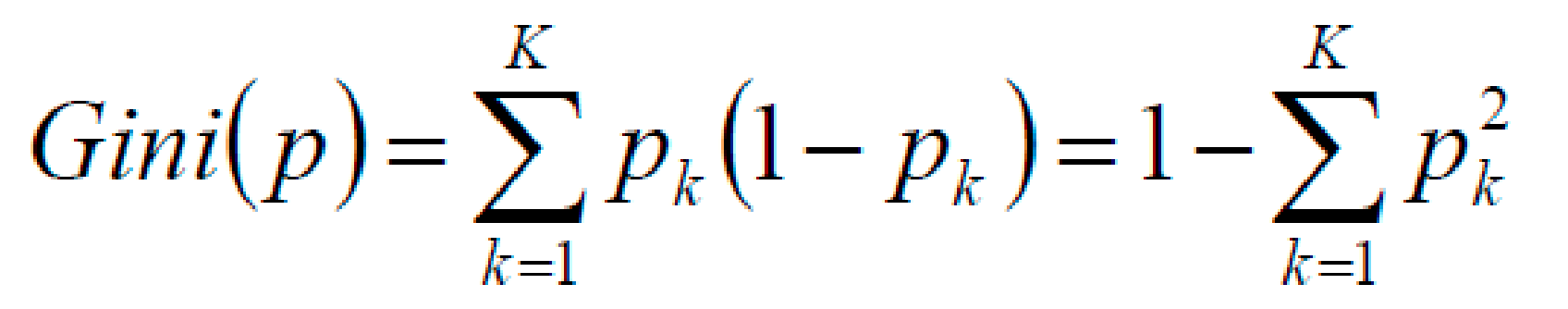
你可以理解成版本迭代即可。
我们来看看现有的解决方法的所存在的问题。
我们把 ID 作为根节点,那对于 ID 来说,有几种划分方式呢?——有 14种,那对于 14种有重复的么?对于 ID 来说没有重复的。那你说,在每一个分支中,只有一个吧。
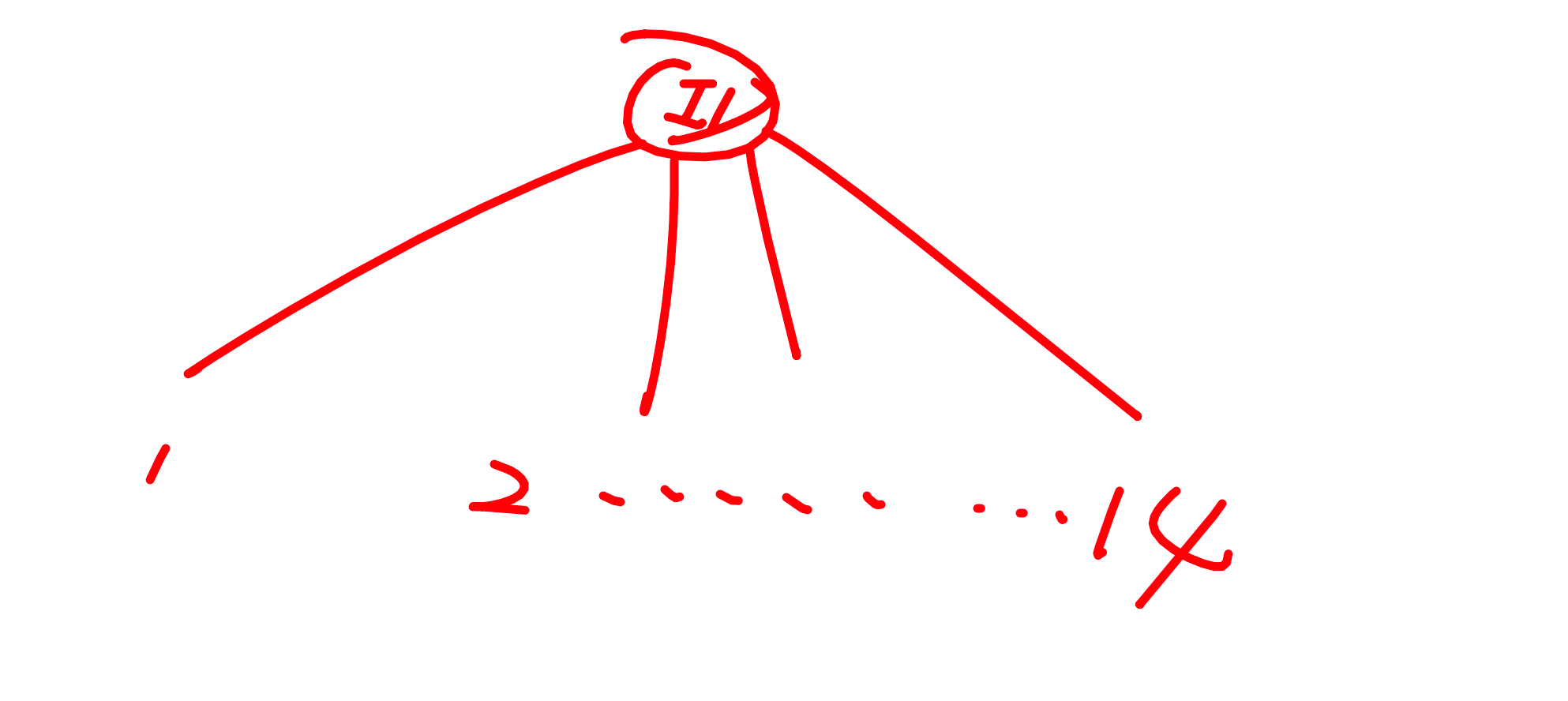
没有重复的,都很纯吧。那去的概率都是百分之百吧,熵值为 0。每个熵值相加还是 0。
熵值等于 0 代表什么?理想状态下,分的最清楚的情况下,熵值才会等于 0 。
那就是说:“ID 这个特征特别有用,把所有样本全分对了。“——太好了吧!我要把它当作根节点。
但是!大家想想,这个 ID 特征有用吗?难道我们从这个编号就能判断打打球么?显然是不行吧。所以说,信息增益它有一个问题,它不适合解决像是 ID 这种特征。「非常稀疏的特征」里面的种类非常非常多的时候,你的信息增益就没办法很好的处理 ID 这种特征了。——这也是 ID3 算法没有用起来是有这样的一个问题。
4.2 C4.5:信息增益率(解决 ID3 问题,考虑自身熵)
就拿上面的 ID 的图来说,这回信息增益用 G 来表示:

我们来看 ID 这个特征本身:它是不是有 14种可能性,那取到每一种的概率比较少,取值 1: ,其他概率也是 。那么 ID 的熵值呢:
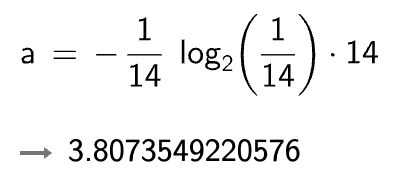
这回我们把信息增益用 G 来表示。
G: 分子:信息增益「原本的和分类后的-差最大」
分母:自身熵值更大。
——整体越小。
所以说 C4.5 算法,信息增益率在一定程度解决了信息增益带来的问题。
4.3 CART:使用 GINI 系数来当做衡量标准
(和熵的衡量标准类似,计算方式不相同)
P 概率最大=1, = 1,1-1=0
P 概率小,多个概率。1-得到的结果也就越小,和我我们的熵值是一样,越小效果越好。
5. 预剪枝方法
欢迎关注我公众号:AI悦创,有更多更好玩的等你发现!
公众号:AI悦创【二维码】

AI悦创·编程一对一
AI悦创·推出辅导班啦,包括「Python 语言辅导班、C++ 辅导班、java 辅导班、算法/数据结构辅导班、少儿编程、pygame 游戏开发」,全部都是一对一教学:一对一辅导 + 一对一答疑 + 布置作业 + 项目实践等。当然,还有线下线上摄影课程、Photoshop、Premiere 一对一教学、QQ、微信在线,随时响应!微信:Jiabcdefh
C++ 信息奥赛题解,长期更新!长期招收一对一中小学信息奥赛集训,莆田、厦门地区有机会线下上门,其他地区线上。微信:Jiabcdefh
方法一:QQ
方法二:微信:Jiabcdefh

更新日志
1c35a-于aed17-于cbb3a-于610fe-于76989-于86c50-于027da-于