算法究竟是个啥东西？

1. 计算机领域的算法

算法，究竟是什么呢？（令人抓耳挠腮，想不明白）

1.1 广义算法

广义而言，做一件事情/解决一个问题的方法，就是算法。

比如：

所有的算法都体现为一个过程：

• 这个过程由若干工序（或称为步骤）组成；
• 这些步骤按照一定的流程来加工某些原料；
• 最终产生某种结果。

当然，要说起来，万事万物都有过程——一个东西放在那里不动还会生锈老化呢，都有“结果“的产出——比如铁锈。你是不是会想，那是不是万事万物皆为算法呢？

所以不用搞得那么玄妙，算法，原本就是人类创造的概念，四季更迭、万物消长这类“上帝的算法”并不在我们的讨论范围内。

我们关心的是：那些能够为我们完成任务或者解决问题的方法。换言之，我们讨论的算法一定有明确的目标，最终的产出也是为了达到目标。

那么总结一下，算法的几个重点要素就是：

1）目标

2）流程

3）原料

4）产出

小贴士：其中的流程是由若干步骤组成的，既然要产出结果，就不能没完没了。所以，流程中的步骤必须是有限的。这一点也叫做算法的有限性。

1.2 狭义的算法

作为广义算法的一个分支，计算机算法自然也具有前面说的几个要素。

广义算法流程的有限性对与计算机算法同样适用，此外，计算机算法的任何步骤都需要：

• 有确切的定义 —— 确定性。
• 能够被分解为计算机可执行的基本操作，并且每个操作都能可以在有限时间内完成 ——可行性。

计算机算法的流程实则是一个有限的操作序列，具体操作通过计算机指令来实现。

至于原料和产出，计算机处理不了面粉布匹，它能处理的只有数据而已。因此，无论是“原料”还是“产出”，于计算机算法而言，都是数据。

所以对于计算机算法而言，我们将原料称为输入数据，简称输入（Input），产出称为输出数据，简称输出（Output）。

那么把上面几点综合起来，计算机算法就是（划重点）：

• 一个有限的、通过计算机指令实现的可执行操作序列；

• 这个序列接受输入；

• 对输入数据进行有限步骤的处理；

• 最终产生确定的输出，用以实现算法的目标。

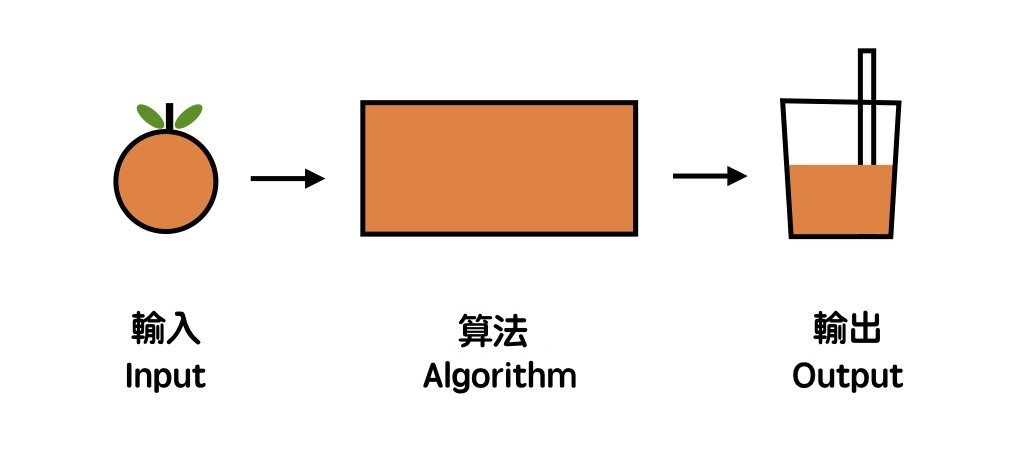
这个定义这么看起来貌似有点乱。没关系，我们可以从内外两个方面来直观地了解一下算法是什么。

小贴士：从现在开始，我们所说的“算法”，如无特殊说明，指的都是计算机算法。

2. 从外面看，一个算法就像一个黑盒

这个黑盒能够解决某一类问题。我们把需要解决的问题作为输入扔到黑盒里面去，里面叮叮哐哐操作一番，过了一段时间之后，从里面倒出来一些输出。这些输出就是对输入对应问题的解答。

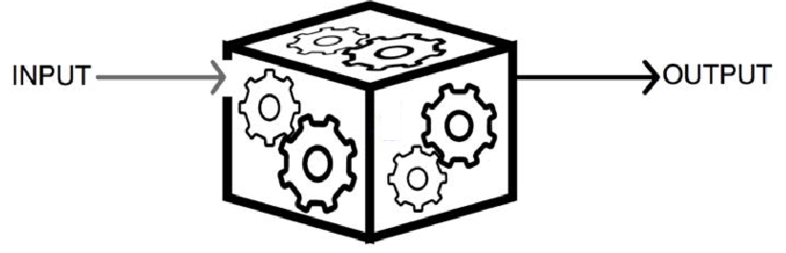
比如：

Case：这个黑盒是用来计算矩形面积的，那么我输入对应一个矩形的长和宽的两个数字，等待片刻（当然，这个片刻短到察觉不到），就得到了一个输出的数字，这就是这个矩形的面积值。

上面这个算法很简单。算法也可以很复杂，比如：

Case： 输入一个用户的个人信息（性别、年龄、所在地、职业、学历等），输出为针对这个用户定制的新闻页面或推荐商品目录或广告列表；

Case：输入用户当前位置和目的地位置，输出一条或多条到达目的地的路线规划和预计时间；

Case：输入一张人脸照片，输出这个人的身份信息；

……

复杂算法的背后可能实际是分成若干更小规模的算法协作实现的。

但无论如何，从外面看起来，总不过是输入问题->运作->输出答案而已。

3. 从内里看，算法 = 数据结构 + 控制流程

数据结构 & 控制流程——又来了两个新名词啊。后面也会有专门的章节分别讲解它们，现在我们只是简单的形象化描述一下而已。

3.1【1】数据结构

我们的算法既然是用来解决一类问题的，那么想必不能够只处理一份数据。

比如：

计算矩形面积的算法，肯定是可以计算长、宽为任意值的矩形的面积的。

不能只会计算长为 10 宽是 5 的矩形面积，当改成长为 37 宽为 82 的时候，它就不会算了。

同样一个算法，要能处理许多“份”数据，那么在算法内部描述对数据的处理时，就不能用确定的数值，而需要用一系列名称来指代各数据——这些用来指代的名称，这个我们叫做变量。

例如：

在计算矩形面积的算法里，我们用变量 length 表示长，用另一个变量 width 表示宽。

那么算法内部，我们只需要计算这两个变量的乘积就可以了——计算的时候，我们不是写 5 x 10，或者 37 x 82，而是写成 length x width。

一个变量一次只能代表一个数吗？

假设：

我们有个算法，计算一个人在一段时间内花费钱财的总和的。

现在我要计算某一户人家在2018年12月的花费。

一看：这些天里爸爸总共花了76笔钱；妈妈花了 569 笔；儿子花了 13 笔。

对应到算法里面，我们怎么来利用变量呢？

用一个变量来指代具体的一笔钱吗？那处理妈妈花费的时候，我们要用 569 个变量吗？

真要这样的话，要统计妈妈一年的花费怎么办？如果妈妈一年花了 73982 笔钱，我们也用 73982 个变量？那计算她十年，二十年，五十年的花费怎么办？

所以这个时候，如果我们能有一种方法来指代“一串”数就好了。这个串可长可短，不管它多长，算法只要把里面的数一个挨着一个的加在一起就行了。

我们用一个变量来指代这个数字“串”，那么花费计算算法里只用一个变量就可以了！

这个时候，我们实际上就规定了一种数据的组织方式——许多具体的数值按照一定的相对位置和相互关系组合起来。比如，在这个花费“串”里，每一笔花费按照时间顺序一个接一个排成一队。

数据的组织方式，就叫做数据结构。

数据结构有很多种，有简单有复杂。上面例子里的结构非常简单，一个个数字排成序列就好了。

上面算法根据这个序列，不仅能算这些花费的总额，还能算平均花销，还可以把单次最高消费找出来。

可是，如果我们要完成的任务变成：

找到单次最高消费是在哪天花的。

就没办法了，因为现有的数据里没有时间信息。

为找到消费对应的时间，可以把每笔钱花出去的日期也“告诉”算法，但是如何告知呢？可以有多种方案，比如：

• 方案-1：用两个序列；第一个是数字序列，每一个数字代表一笔花销，第二个是时间序列，每一个时间表示花费一笔钱的时间点；这两个序列中的元素按照在序列中的位置一 一对应。
• 方案-2：只采用一个序列，不过这个序列中每个元素包含两个部分：时间和金额。

上述两个方案所对应的数据结构就是不同的。

如果我们还想看到：

每笔钱花在了什么地方？给了哪个商家？购买了什么产品或者服务？

那就需要把更多的信息“告诉”算法，采用的数据结构也就会更加复杂。

3.2 【2】控制流程

回到前面的花销计算算法：计算“一个人在一段时间内花费钱财的总和”，选定用一个数字序列作为数据结构。

这个算法：

• 接受一个数字序列作为输入；
• 把这个序列里面的数字一个个“拿出来”；
• 将拿出来的数值累加在一起；
• 将最终的累加和结果输出出来。

整个过程有始有终，运行的顺序清晰明确，这就是控制流程。

控制流程的定义很简单：程序运行的步骤历程，就是控制流程。

对应不同的数据结构，当然有不同的处理方法。

**算法的控制流程往往和数据结构有关系。**换言之，同样目标的算法，因为所采用的数据结构不同，很可能会造成运行、求值的步骤顺序的不同。

欢迎关注我公众号：AI悦创，有更多更好玩的等你发现！

公众号：AI悦创【二维码】