Binary Tree
你好,我是悦创。
二叉树(Binary Tree)是一种非线性数据结构,代表“祖先”与“后代”之间的派生关系,体现了“一分为二”的分治逻辑。与链表类似,二叉树的基本单元是节点,每个节点包含值、左子节点引用和右子节点引用。
class TreeNode:
"""二叉树节点类"""
def __init__(self, val: int):
self.val: int = val # 节点值
self.left: TreeNode | None = None # 左子节点引用
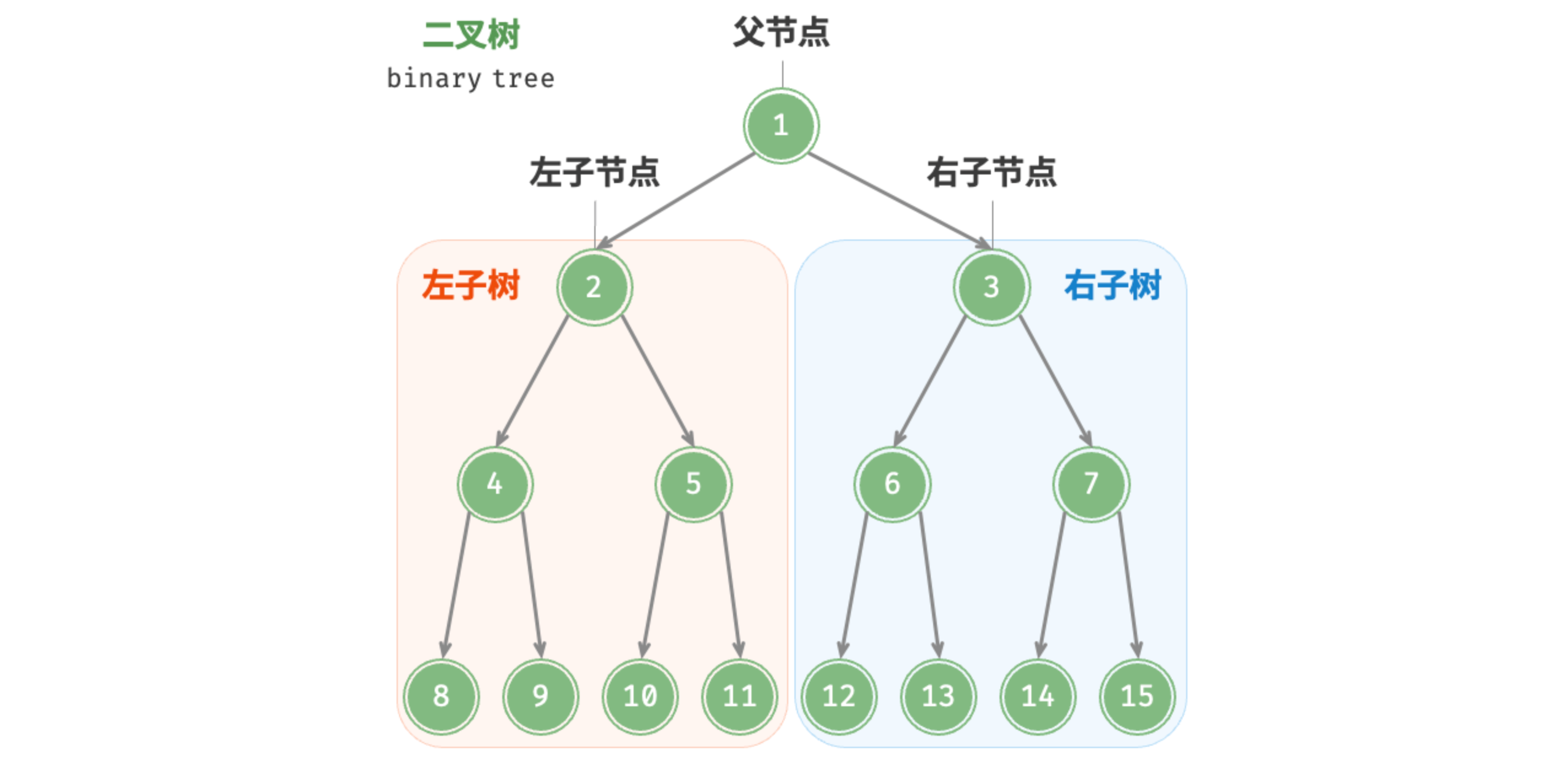
self.right: TreeNode | None = None # 右子节点引用每个节点都有两个引用(指针),分别指向左子节点(left-child node)和右子节点(right-child node),该节点被称为这两个子节点的父节点(parent node)。当给定一个二叉树的节点时,我们将该节点的左子节点及其以下节点形成的树称为该节点的左子树(left subtree),同理可得右子树(right subtree)。
在二叉树中,除叶节点外,其他所有节点都包含子节点和非空子树。如图 7-1 所示,如果将“节点 2”视为父节点,则其左子节点和右子节点分别是“节点 4”和“节点 5”,左子树是“节点 4 及其以下节点形成的树”,右子树是“节点 5 及其以下节点形成的树”。
1. 常见的术语
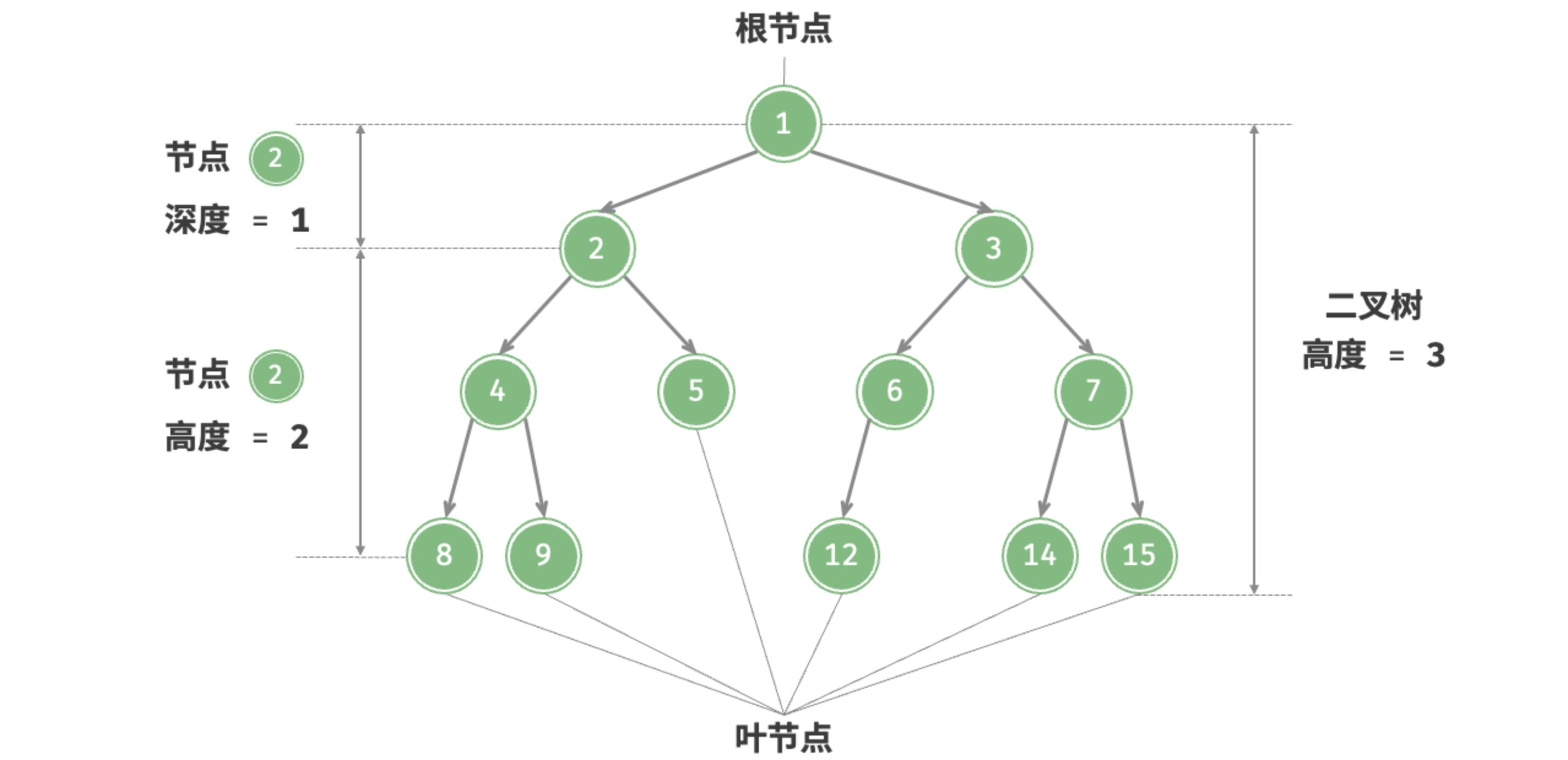
二叉树的常用术语如图 7-2 所示。
- 根节点(root node):位于二叉树顶层的节点,没有父节点。
- 叶节点(leaf node):没有子节点的节点,其两个指针均指向
None。 - 边(edge):连接两个节点的线段,即节点引用(指针)。
- 节点所在的层(level):从顶至底递增,根节点所在层为 1 。
- 节点的度(degree):节点的子节点的数量。在二叉树中,度的取值范围是 0、1、2 。
- 二叉树的高度(height):从根节点到最远叶节点所经过的边的数量。
- 节点的深度(depth):从根节点到该节点所经过的边的数量。
- 节点的高度(height):从距离该节点最远的叶节点到该节点所经过的边的数量。
注意
请注意,我们通常将“高度”和“深度”定义为“经过的边的数量”,但有些题目或教材可能会将其定义为“经过的节点的数量”。在这种情况下,高度和深度都需要加 1 。
2. 二叉树基本操作
2.1 初始化二叉树
与链表类似,首先初始化节点,然后构建引用(指针)。
# 初始化二叉树
# 初始化节点
n1 = TreeNode(val=1)
n2 = TreeNode(val=2)
n3 = TreeNode(val=3)
n4 = TreeNode(val=4)
n5 = TreeNode(val=5)
# 构建节点之间的引用(指针)
n1.left = n2
n1.right = n3
n2.left = n4
n2.right = n52.2 插入与删除节点
与链表类似,在二叉树中插入与删除节点可以通过修改指针来实现。图 7-3 给出了一个示例。
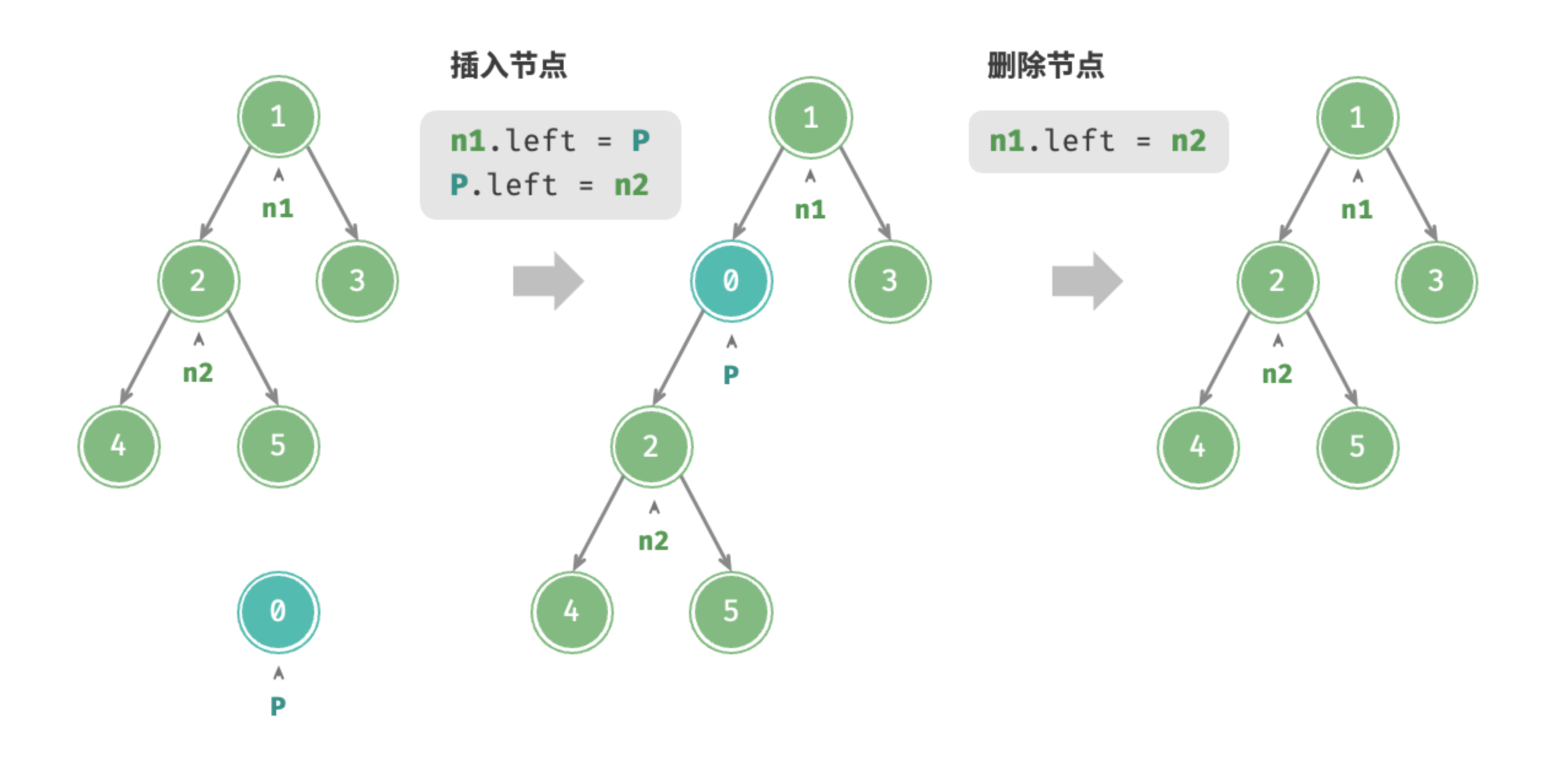
# 插入与删除节点
p = TreeNode(0)
# 在 n1 -> n2 中间插入节点 P
n1.left = p
p.left = n2
# 删除节点 P
n1.left = n2提示
需要注意的是,插入节点可能会改变二叉树的原有逻辑结构,而删除节点通常意味着删除该节点及其所有子树。因此,在二叉树中,插入与删除通常是由一套操作配合完成的,以实现有实际意义的操作。
3. 常见二叉树类型
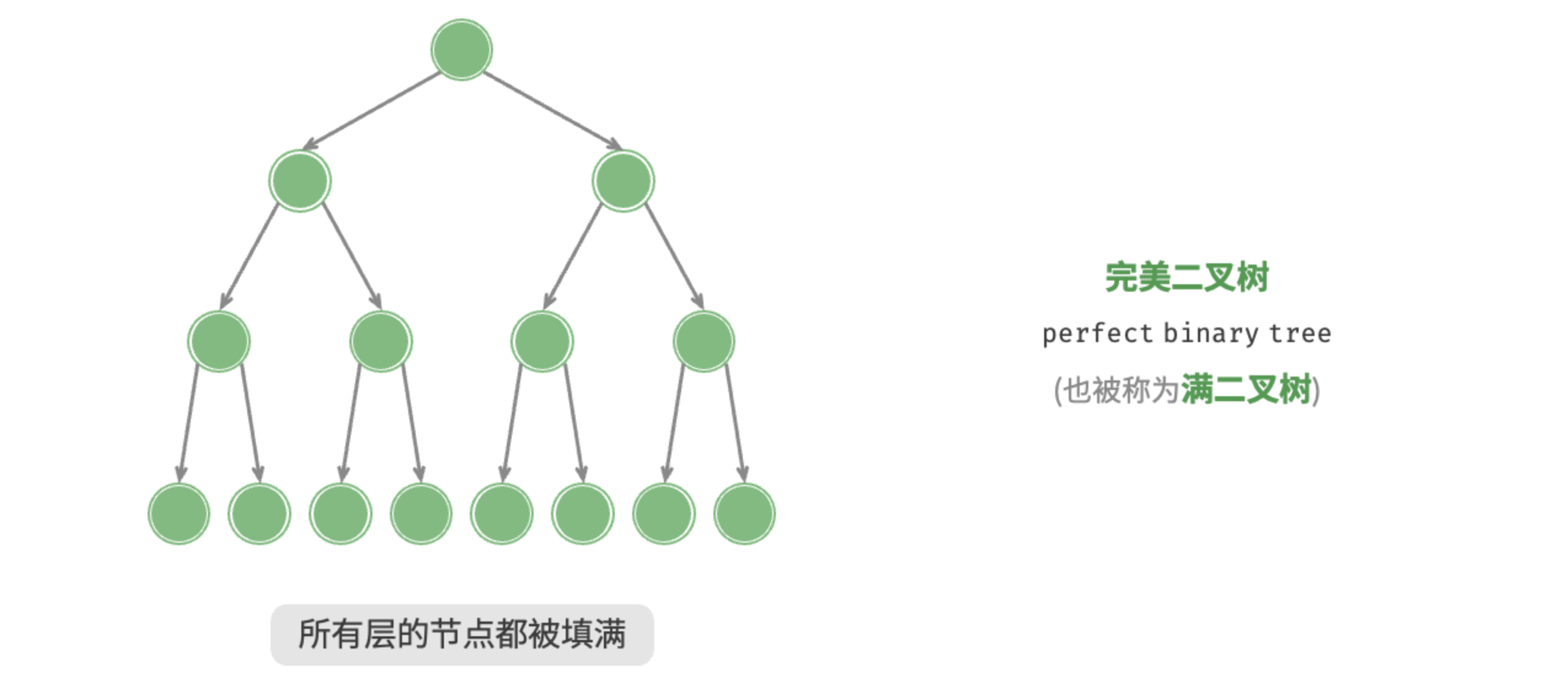
3.1 完美二叉树
如图 7-4 所示,完美二叉树(perfect binary tree)所有层的节点都被完全填满。在完美二叉树中,叶节点的度为 0 ,其余所有节点的度都为 2;若树的高度为 h,则节点总数为 ,呈现标准的指数级关系,反映了自然界中常见的细胞分裂现象。
提示
请注意,在中文社区中,完美二叉树常被称为满二叉树。
3.2 完全二叉树
如图 7-5 所示,完全二叉树(complete binary tree)只有最底层的节点未被填满,且最底层节点尽量靠左填充。
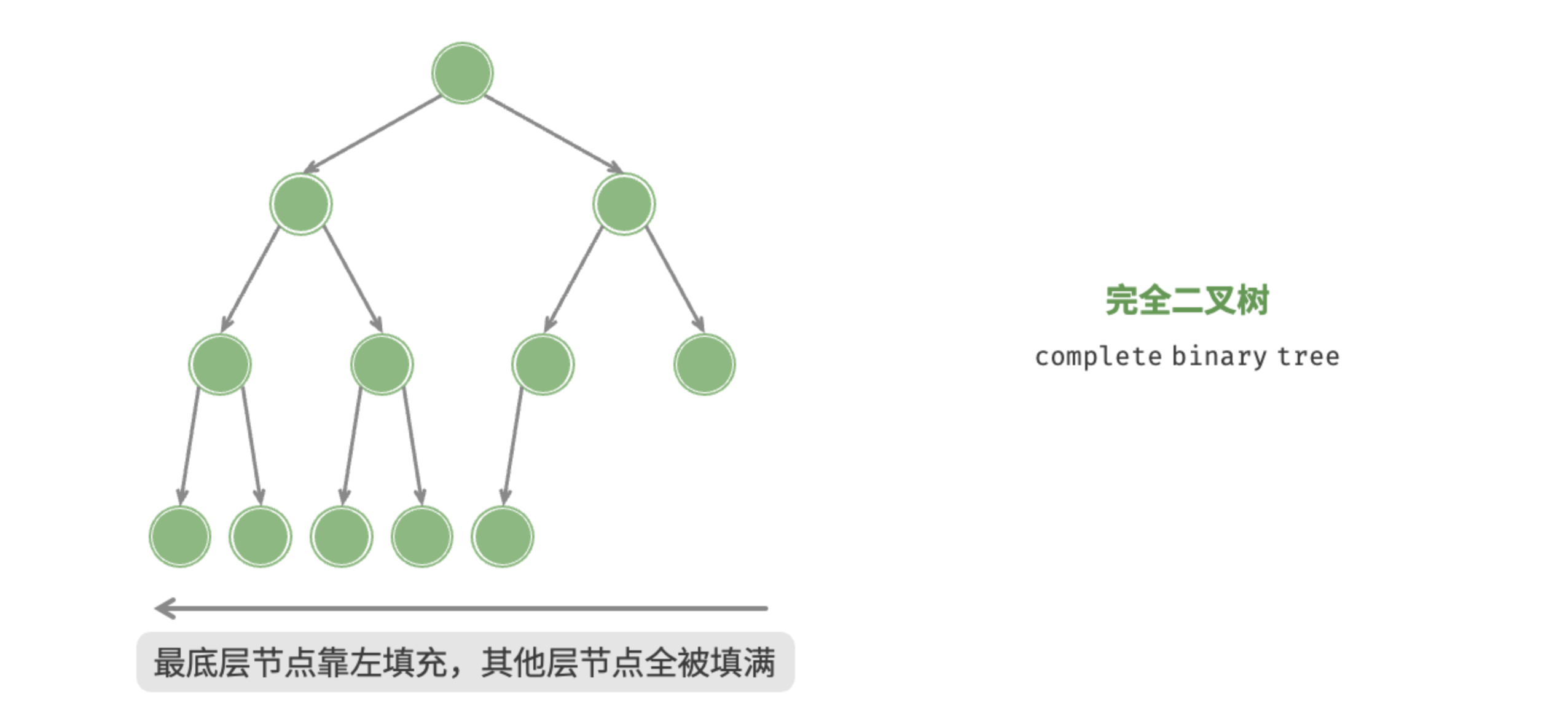
3.3 完满二叉树
如图 7-6 所示,完满二叉树(full binary tree)除了叶节点之外,其余所有节点都有两个子节点。
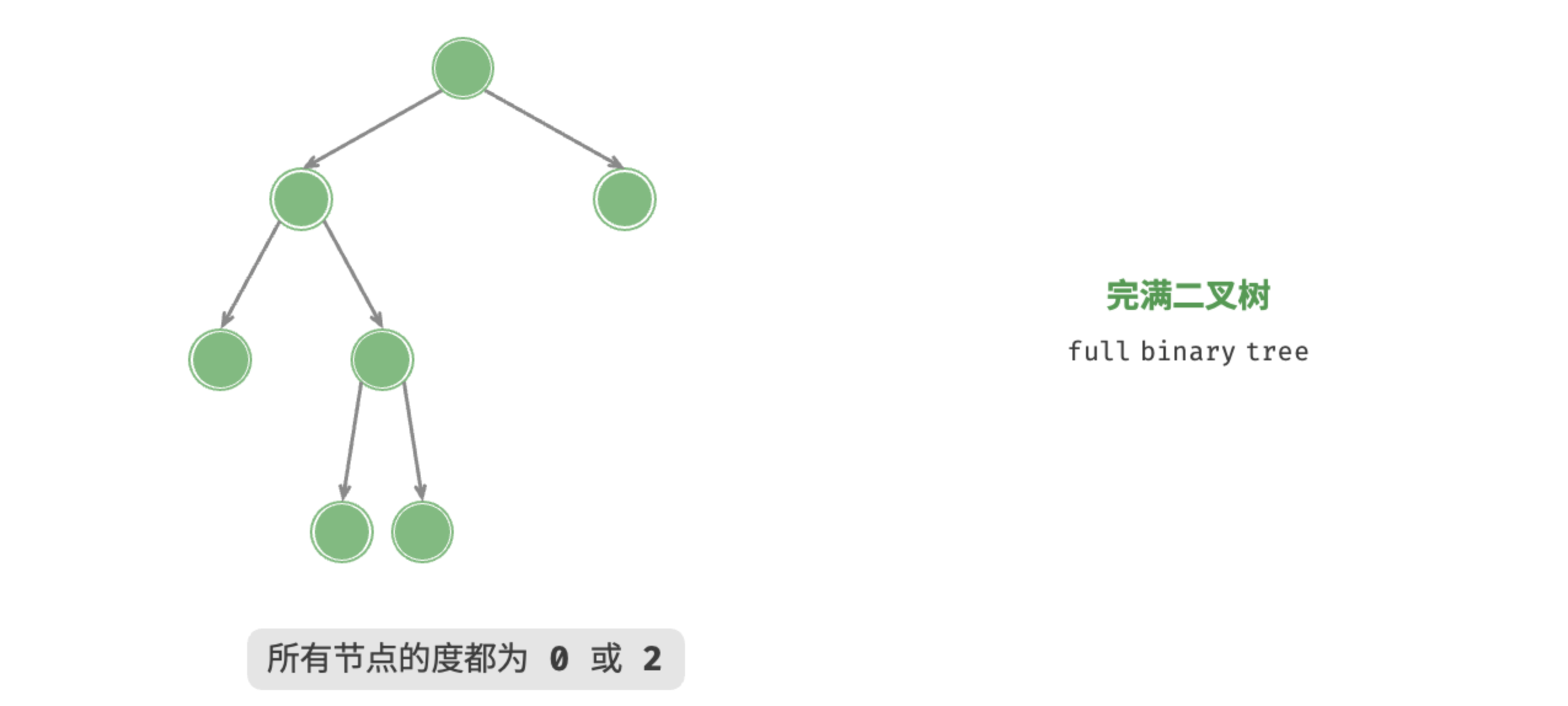
3.4 平衡二叉树
如图 7-7 所示,平衡二叉树(balanced binary tree)中任意节点的左子树和右子树的高度之差的绝对值不超过 1 。
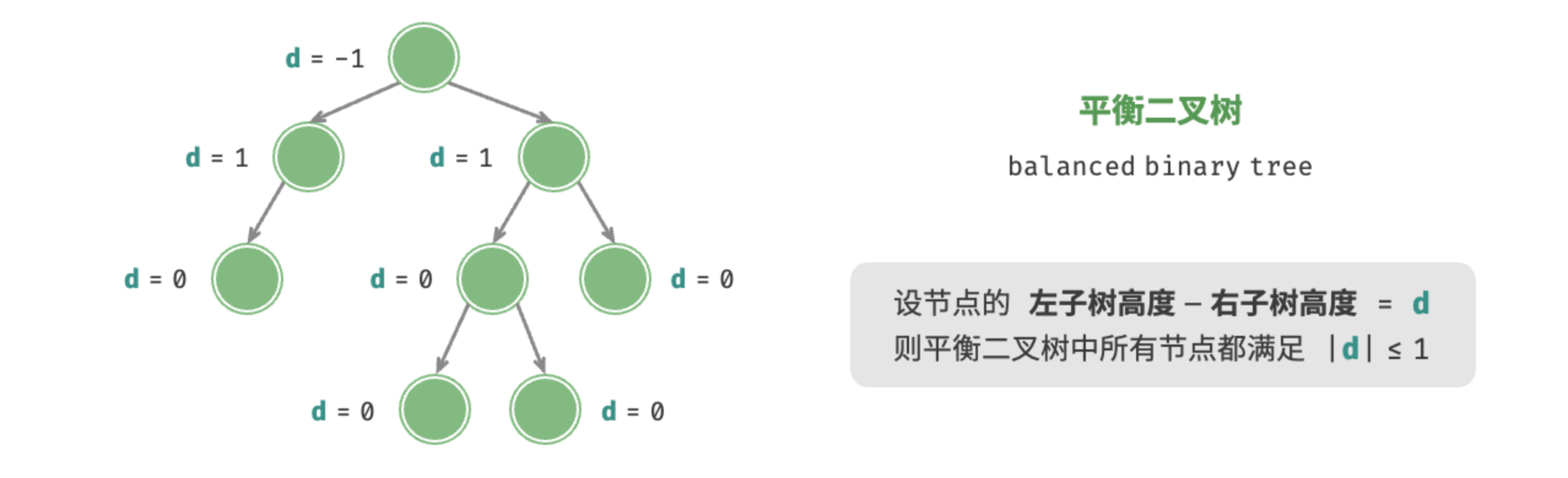
4. 二叉树的退化
图 7-8 展示了二叉树的理想结构与退化结构。当二叉树的每层节点都被填满时,达到“完美二叉树”;而当所有节点都偏向一侧时,二叉树退化为“链表”。
- 完美二叉树是理想情况,可以充分发挥二叉树“分治”的优势。
- 链表则是另一个极端,各项操作都变为线性操作,时间复杂度退化至 。
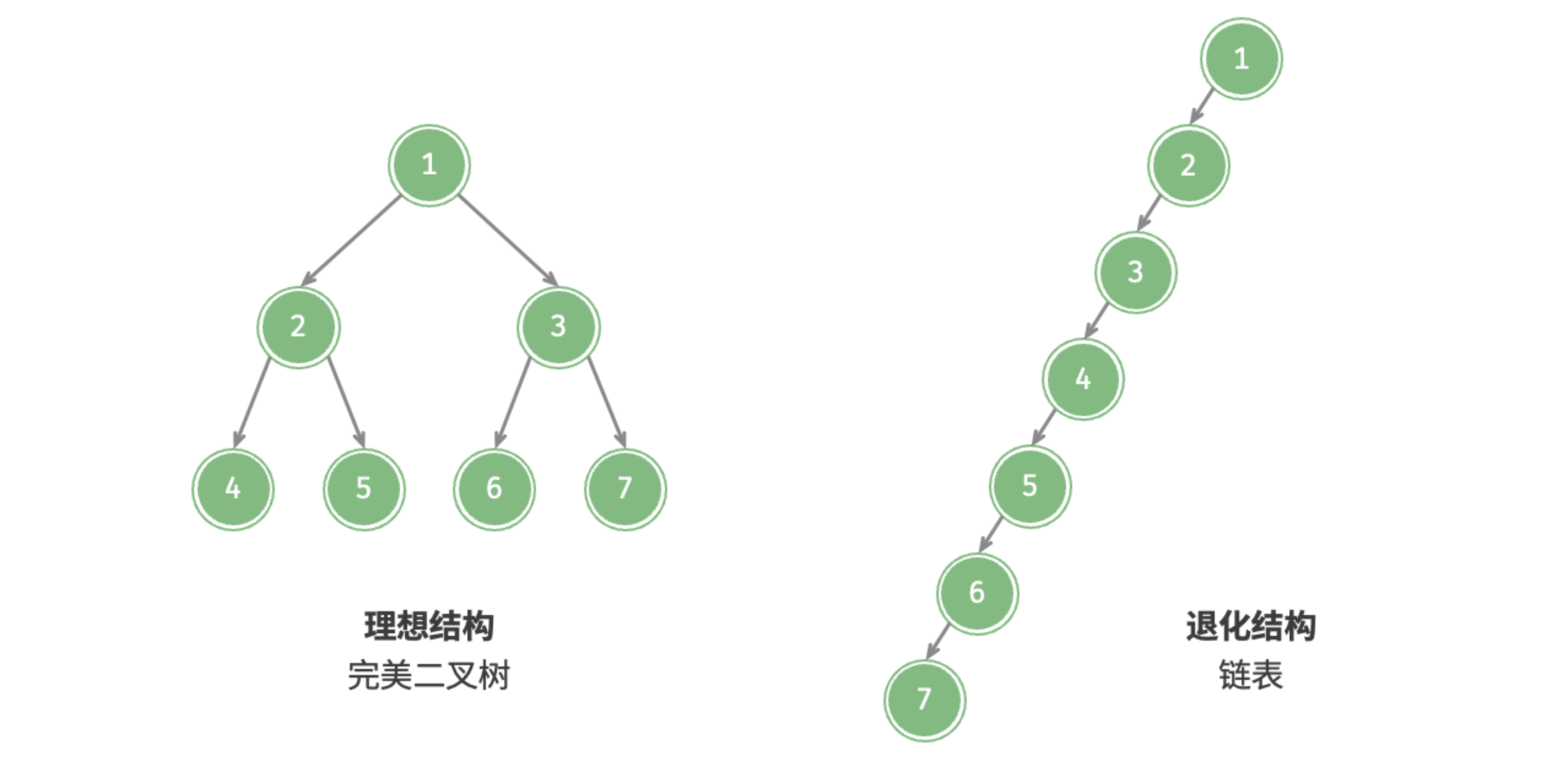
如表 7-1 所示,在最佳结构和最差结构下,二叉树的叶节点数量、节点总数、高度等达到极大值或极小值。
表 7-1 二叉树的最佳结构与最差结构
| 完美二叉树 | 链表 | |
|---|---|---|
| 第 层的节点数量 | ||
| 高度为 的树的叶节点数量 | ||
| 高度为 的树的节点总数 | ||
| 节点总数为 的树的高度 |
5. 可视化二叉树代码
class TreeNode:
"""二叉树节点类"""
def __init__(self, val: int):
self.val: int = val # 节点值
self.left: 'TreeNode' | None = None # 左子节点引用
self.right: 'TreeNode' | None = None # 右子节点引用
def display(root):
"""打印二叉树为字符树"""
lines, *_ = _display_aux(root)
for line in lines:
print(line)
def _display_aux(node):
"""返回包含当前子树所有行的列表,以及子树宽度、高度和水平坐标"""
if node is None:
return [" "], 0, 0, 0
line = f'{node.val}'
width = len(line)
height = 1
middle = width // 2
# 只有左子树
if node.left and not node.right:
l_lines, l_width, l_height, l_middle = _display_aux(node.left)
first_line = ' ' * (l_middle + 1) + '_' * (l_width - l_middle - 1) + line
second_line = ' ' * l_middle + '/' + ' ' * (l_width - l_middle - 1 + width)
shifted_lines = [line + ' ' * width for line in l_lines]
return [first_line, second_line] + shifted_lines, l_width + width, l_height + 2, l_width + width // 2
# 只有右子树
if not node.left and node.right:
r_lines, r_width, r_height, r_middle = _display_aux(node.right)
first_line = line + '_' * r_middle + ' ' * (r_width - r_middle)
second_line = ' ' * (width + r_middle) + '\\' + ' ' * (r_width - r_middle - 1)
shifted_lines = [' ' * width + line for line in r_lines]
return [first_line, second_line] + shifted_lines, width + r_width, r_height + 2, width // 2
# 同时有左右子树
if node.left and node.right:
l_lines, l_width, l_height, l_middle = _display_aux(node.left)
r_lines, r_width, r_height, r_middle = _display_aux(node.right)
first_line = ' ' * (l_middle + 1) + '_' * (l_width - l_middle - 1) + line + '_' * r_middle + ' ' * (r_width - r_middle)
second_line = ' ' * l_middle + '/' + ' ' * (l_width - l_middle - 1 + width + r_middle) + '\\' + ' ' * (r_width - r_middle - 1)
# 对齐高度
if l_height < r_height:
l_lines += [' ' * l_width] * (r_height - l_height)
elif r_height < l_height:
r_lines += [' ' * r_width] * (l_height - r_height)
merged_lines = [a + ' ' * width + b for a, b in zip(l_lines, r_lines)]
return [first_line, second_line] + merged_lines, l_width + width + r_width, max(l_height, r_height) + 2, l_width + width // 2
# 叶子节点
return [line], width, height, middle
# 示例:创建二叉树并打印
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
root.right.right = TreeNode(6)
display(root)
# --------
n1 = TreeNode(1)
n2 = TreeNode(2)
n3 = TreeNode(3)
n4 = TreeNode(4)
n5 = TreeNode(5)
n1.left = n2
n1.right = n3
n2.left = n4
n2.right = n5
p = TreeNode(0)
n1.left = p
p.left = n2
display(n1)class TreeNode:
"""二叉树节点类"""
def __init__(self, val: int):
self.val: int = val # 节点的值
self.left: 'TreeNode' | None = None # 左子节点,初始为 None
self.right: 'TreeNode' | None = None # 右子节点,初始为 None
def display(root):
"""打印二叉树为字符树"""
lines, *_ = _display_aux(root) # 调用辅助函数,获取打印所需的行列表
for line in lines:
print(line) # 逐行打印
def _display_aux(node):
"""
辅助递归函数,返回表示二叉树的字符串行列表,以及子树的宽度、高度和根节点在宽度中的偏移量
"""
if node is None:
# 如果节点为空,返回一个空格,占位
return [" "], 0, 0, 0
line = f'{node.val}' # 将节点的值转换为字符串
width = len(line) # 当前行的宽度,即节点值的字符数
height = 1 # 当前子树的高度,初始为 1
middle = width // 2 # 根节点在当前行中的中间位置
# 情况 1:只有左子树
if node.left and not node.right:
l_lines, l_width, l_height, l_middle = _display_aux(node.left) # 递归左子树
# 第一行:在左子树上方添加连接线,连接到当前节点
first_line = ' ' * (l_middle + 1) + '_' * (l_width - l_middle - 1) + line
# 第二行:在左子树和当前节点之间添加斜杠,表示连接
second_line = ' ' * l_middle + '/' + ' ' * (l_width - l_middle - 1 + width)
# 调整左子树的行,使其右移,和当前节点对齐
shifted_lines = [line + ' ' * width for line in l_lines]
# 返回合并后的行列表,更新宽度和高度信息
return [first_line, second_line] + shifted_lines, l_width + width, l_height + 2, l_width + width // 2
# 情况 2:只有右子树
if not node.left and node.right:
r_lines, r_width, r_height, r_middle = _display_aux(node.right) # 递归右子树
# 第一行:在当前节点后添加连接线,连接到右子树
first_line = line + '_' * r_middle + ' ' * (r_width - r_middle)
# 第二行:在当前节点和右子树之间添加反斜杠,表示连接
second_line = ' ' * (width + r_middle) + '\\' + ' ' * (r_width - r_middle - 1)
# 调整右子树的行,使其左移,和当前节点对齐
shifted_lines = [' ' * width + line for line in r_lines]
# 返回合并后的行列表,更新宽度和高度信息
return [first_line, second_line] + shifted_lines, width + r_width, r_height + 2, width // 2
# 情况 3:同时有左、右子树
if node.left and node.right:
l_lines, l_width, l_height, l_middle = _display_aux(node.left) # 递归左子树
r_lines, r_width, r_height, r_middle = _display_aux(node.right) # 递归右子树
# 第一行:连接左子树、当前节点和右子树的连接线
first_line = ' ' * (l_middle + 1) + '_' * (l_width - l_middle - 1) + line + '_' * r_middle + ' ' * (r_width - r_middle)
# 第二行:在左子树和当前节点之间添加斜杠,在当前节点和右子树之间添加反斜杠
second_line = ' ' * l_middle + '/' + ' ' * (l_width - l_middle - 1 + width + r_middle) + '\\' + ' ' * (r_width - r_middle - 1)
# 如果左子树高度小于右子树,高度对齐,左子树补充空行
if l_height < r_height:
l_lines += [' ' * l_width] * (r_height - l_height)
# 如果右子树高度小于左子树,高度对齐,右子树补充空行
elif r_height < l_height:
r_lines += [' ' * r_width] * (l_height - r_height)
# 合并左、右子树的行列表,每行之间加上当前节点的间隔
merged_lines = [a + ' ' * width + b for a, b in zip(l_lines, r_lines)]
# 返回完整的行列表,更新宽度和高度信息
return [first_line, second_line] + merged_lines, l_width + width + r_width, max(l_height, r_height) + 2, l_width + width // 2
# 情况 4:叶子节点(没有子节点)
return [line], width, height, middle # 返回节点值行,及其宽度和高度信息
# 示例:创建二叉树并打印
root = TreeNode(1) # 根节点 1
root.left = TreeNode(2) # 左子节点 2
root.right = TreeNode(3) # 右子节点 3
root.left.left = TreeNode(4) # 节点 2 的左子节点 4
root.left.right = TreeNode(5) # 节点 2 的右子节点 5
root.right.right = TreeNode(6) # 节点 3 的右子节点 6
display(root) # 打印二叉树6. 二叉树遍历
从物理结构的角度来看,树是一种基于链表的数据结构,因此其遍历方式是通过指针逐个访问节点。然而,树是一种非线性数据结构,这使得遍历树比遍历链表更加复杂,需要借助搜索算法来实现。
二叉树常见的遍历方式包括层序遍历、前序遍历、中序遍历和后序遍历等。
6.1 层序遍历
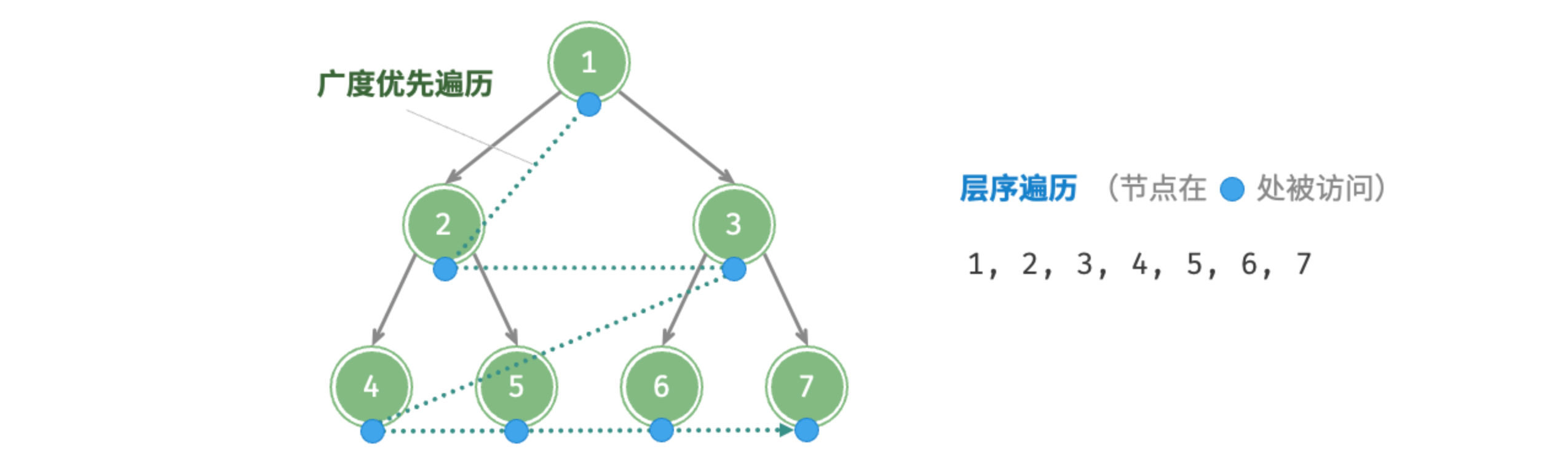
如图 7-9 所示,层序遍历(level-order traversal)从顶部到底部逐层遍历二叉树,并在每一层按照从左到右的顺序访问节点。
层序遍历本质上属于广度优先遍历(breadth-first traversal),也称广度优先搜索(breadth-first search, BFS),它体现了一种“一圈一圈向外扩展”的逐层遍历方式。
6.1.1 代码实现
广度优先遍历通常借助“队列”来实现。队列遵循“先进先出”的规则,而广度优先遍历则遵循“逐层推进”的规则,两者背后的思想是一致的。实现代码如下:
def level_order(root: TreeNode | None) -> list[int]:
"""层序遍历"""
# 初始化队列,加入根节点
queue: deque[TreeNode] = deque()
queue.append(root)
# 初始化一个列表,用于保存遍历序列
res = []
while queue:
node: TreeNode = queue.popleft() # 队列出队
res.append(node.val) # 保存节点值
if node.left is not None:
queue.append(node.left) # 左子节点入队
if node.right is not None:
queue.append(node.right) # 右子节点入队
return resdef level_order(root: TreeNode | None) -> list[int]:
"""层序遍历,使用列表实现队列"""
# 初始化一个列表作为队列,加入根节点
queue: list[TreeNode] = []
if root is not None:
queue.append(root)
# 初始化一个列表,用于保存遍历序列
res = []
# 当队列不为空时,进行循环
while queue:
# 从列表的第一个元素处取出节点,模拟队列的出队操作
node: TreeNode = queue.pop(0) # 列表第一个元素出列
# 保存当前节点的值
res.append(node.val)
# 如果左子节点不为空,加入列表末尾,模拟队列的入队操作
if node.left is not None:
queue.append(node.left)
# 如果右子节点不为空,同样加入列表末尾
if node.right is not None:
queue.append(node.right)
# 返回结果列表
return resdef level_order_recursive(root: TreeNode | None) -> list[int]:
"""递归实现层序遍历"""
def traverse_level(nodes: list[TreeNode], res: list[int]) -> None:
"""递归遍历当前层节点,并将下一层节点传入"""
if not nodes: # 如果当前层为空,停止递归
return
# 保存当前层所有节点的值
res.extend([node.val for node in nodes])
# 收集下一层的所有节点
next_level = [child for node in nodes for child in (node.left, node.right) if child]
# 递归处理下一层
traverse_level(next_level, res)
# 初始化结果列表
res = []
# 从根节点开始处理第一层
if root:
traverse_level([root], res)
return resdef printtree(root):
queue = []
queue.append(root)
res = []
while queue:
length = len(queue)
for i in range(length):
node = queue[i]
res.append(node.val)
if node.left is not None:
queue.append(node.left)
if node.right is not None:
queue.append(node.right)
queue = queue[length:]
return resclass TreeNode:
def __init__(self, value=0, left=None, right=None):
self.val = value
self.left = left
self.right = right
def level_order_recursive(root: TreeNode) -> list:
def traverse_level(nodes: list, result: list):
if not nodes: # 如果当前层没有节点,停止递归
return
current_values = [] # 用来存储当前层的值
next_level_nodes = [] # 用来存储下一层的节点
# 遍历当前层的所有节点
for node in nodes:
current_values.append(node.val) # 保存当前节点的值
# 将左右子节点加入下一层的节点列表
if node.left:
next_level_nodes.append(node.left)
if node.right:
next_level_nodes.append(node.right)
result.append(current_values) # 保存当前层的所有节点值
traverse_level(next_level_nodes, result) # 递归处理下一层
result = []
if root:
traverse_level([root], result) # 从根节点开始递归
return result
"""
1
/ \
2 3
/ \ \
4 5 6
[[1], [2, 3], [4, 5, 6]]
"""class TreeNode:
def __init__(self, value=0, left=None, right=None):
self.val = value
self.left = left
self.right = right
def level_order_recursive(root: TreeNode) -> list:
result = [] # 用来存储最终的层序遍历结果
level_order_helper([root], result) # 从根节点开始递归
return result
def level_order_helper(nodes: list, result: list):
if not nodes or all(node is None for node in nodes): # 如果当前层没有节点,停止递归
return
current_values = [] # 存储当前层的节点值
next_level_nodes = [] # 存储下一层的节点
# 遍历当前层的所有节点
for node in nodes:
if node: # 检查节点是否为None
current_values.append(node.val) # 记录当前节点的值
# 将左右子节点加入下一层节点列表
if node.left:
next_level_nodes.append(node.left)
if node.right:
next_level_nodes.append(node.right)
# 如果当前层有值,保存结果
if current_values:
result.append(current_values)
# 递归处理下一层的节点
level_order_helper(next_level_nodes, result)class TreeNode:
def __init__(self, value=0, left=None, right=None):
self.val = value
self.left = left
self.right = right
def level_order_recursive(root: TreeNode) -> list:
res = [] # 存储遍历结果
if root:
level_order_helper([root], res) # 从根节点开始递归
return res
def level_order_helper(queue: list, res: list):
if not queue: # 当队列为空时,递归终止
return
# 处理当前节点
node = queue.pop(0)
res.append(node)
# 递归处理左子树
if node.left is not None:
queue.append(node.left)
# 递归处理右子树
if node.right is not None:
queue.append(node.right)
# 递归调用处理下一层
level_order_helper(queue, res)def level_order(root):
if not res:
res.append(root.val)
if root.left:
res.append(root.left.val)
if root.right:
res.append(root.right.val)
if root.left is not None:
level_order(root.left)
if root.right is not None:
level_order(root.right)/* 层序遍历 */
vector<int> levelOrder(TreeNode *root) {
// 初始化队列,加入根节点
queue<TreeNode *> queue;
queue.push(root);
// 初始化一个列表,用于保存遍历序列
vector<int> vec;
while (!queue.empty()) {
TreeNode *node = queue.front();
queue.pop(); // 队列出队
vec.push_back(node->val); // 保存节点值
if (node->left != nullptr)
queue.push(node->left); // 左子节点入队
if (node->right != nullptr)
queue.push(node->right); // 右子节点入队
}
return vec;
}/* 层序遍历 */
List<Integer> levelOrder(TreeNode root) {
// 初始化队列,加入根节点
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
// 初始化一个列表,用于保存遍历序列
List<Integer> list = new ArrayList<>();
while (!queue.isEmpty()) {
TreeNode node = queue.poll(); // 队列出队
list.add(node.val); // 保存节点值
if (node.left != null)
queue.offer(node.left); // 左子节点入队
if (node.right != null)
queue.offer(node.right); // 右子节点入队
}
return list;
}/* 层序遍历 */
List<int> LevelOrder(TreeNode root) {
// 初始化队列,加入根节点
Queue<TreeNode> queue = new();
queue.Enqueue(root);
// 初始化一个列表,用于保存遍历序列
List<int> list = [];
while (queue.Count != 0) {
TreeNode node = queue.Dequeue(); // 队列出队
list.Add(node.val!.Value); // 保存节点值
if (node.left != null)
queue.Enqueue(node.left); // 左子节点入队
if (node.right != null)
queue.Enqueue(node.right); // 右子节点入队
}
return list;
}
6.1.2 复杂度分析
- 时间复杂度为 :所有节点被访问一次,使用 时间,其中 为节点数量。
- 空间复杂度为 :在最差情况下,即满二叉树时,遍历到最底层之前,队列中最多同时存在 个节点,占用 空间。
6.2 前序、中序、后序遍历
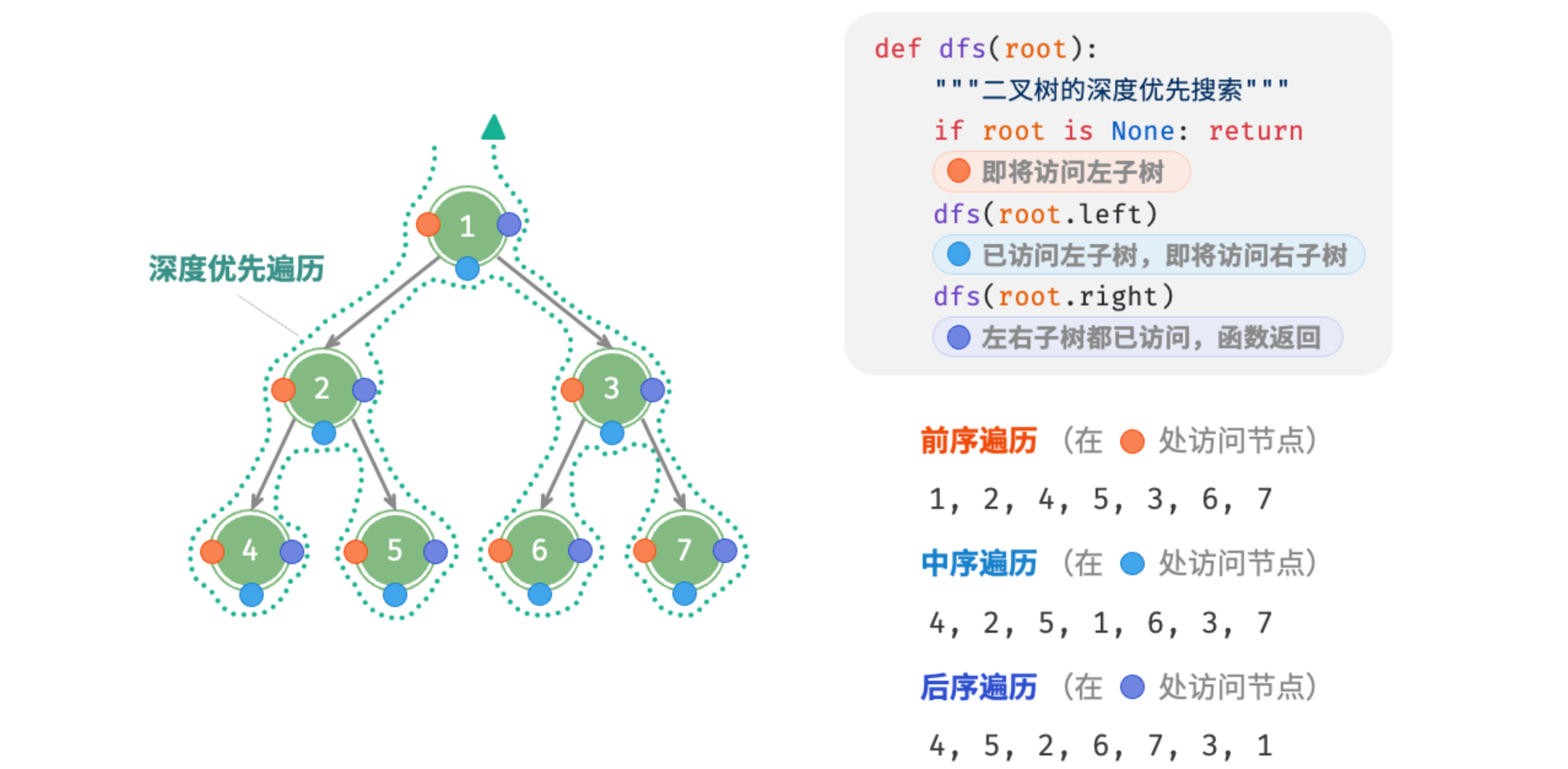
相应地,前序、中序和后序遍历都属于深度优先遍历(depth-first traversal),也称深度优先搜索(depth-first search, DFS),它体现了一种“先走到尽头,再回溯继续”的遍历方式。
图 7-10 展示了对二叉树进行深度优先遍历的工作原理。深度优先遍历就像是绕着整棵二叉树的外围“走”一圈,在每个节点都会遇到三个位置,分别对应前序遍历、中序遍历和后序遍历。
6.2.1 代码实现
深度优先搜索通常基于递归实现:
def pre_order(root: TreeNode | None):
"""前序遍历"""
if root is None:
return
# 访问优先级:根节点 -> 左子树 -> 右子树
res.append(root.val)
pre_order(root=root.left)
pre_order(root=root.right)
def in_order(root: TreeNode | None):
"""中序遍历"""
if root is None:
return
# 访问优先级:左子树 -> 根节点 -> 右子树
in_order(root=root.left)
res.append(root.val)
in_order(root=root.right)
def post_order(root: TreeNode | None):
"""后序遍历"""
if root is None:
return
# 访问优先级:左子树 -> 右子树 -> 根节点
post_order(root=root.left)
post_order(root=root.right)
res.append(root.val)/* 前序遍历 */
void preOrder(TreeNode *root) {
if (root == nullptr)
return;
// 访问优先级:根节点 -> 左子树 -> 右子树
vec.push_back(root->val);
preOrder(root->left);
preOrder(root->right);
}
/* 中序遍历 */
void inOrder(TreeNode *root) {
if (root == nullptr)
return;
// 访问优先级:左子树 -> 根节点 -> 右子树
inOrder(root->left);
vec.push_back(root->val);
inOrder(root->right);
}
/* 后序遍历 */
void postOrder(TreeNode *root) {
if (root == nullptr)
return;
// 访问优先级:左子树 -> 右子树 -> 根节点
postOrder(root->left);
postOrder(root->right);
vec.push_back(root->val);
}/* 前序遍历 */
void preOrder(TreeNode root) {
if (root == null)
return;
// 访问优先级:根节点 -> 左子树 -> 右子树
list.add(root.val);
preOrder(root.left);
preOrder(root.right);
}
/* 中序遍历 */
void inOrder(TreeNode root) {
if (root == null)
return;
// 访问优先级:左子树 -> 根节点 -> 右子树
inOrder(root.left);
list.add(root.val);
inOrder(root.right);
}
/* 后序遍历 */
void postOrder(TreeNode root) {
if (root == null)
return;
// 访问优先级:左子树 -> 右子树 -> 根节点
postOrder(root.left);
postOrder(root.right);
list.add(root.val);
}/* 前序遍历 */
void PreOrder(TreeNode? root) {
if (root == null) return;
// 访问优先级:根节点 -> 左子树 -> 右子树
list.Add(root.val!.Value);
PreOrder(root.left);
PreOrder(root.right);
}
/* 中序遍历 */
void InOrder(TreeNode? root) {
if (root == null) return;
// 访问优先级:左子树 -> 根节点 -> 右子树
InOrder(root.left);
list.Add(root.val!.Value);
InOrder(root.right);
}
/* 后序遍历 */
void PostOrder(TreeNode? root) {
if (root == null) return;
// 访问优先级:左子树 -> 右子树 -> 根节点
PostOrder(root.left);
PostOrder(root.right);
list.Add(root.val!.Value);
}提示
深度优先搜索也可以基于迭代实现,有兴趣的读者可以自行研究。
图 7-11 展示了前序遍历二叉树的递归过程,其可分为“递”和“归”两个逆向的部分。
- “递”表示开启新方法,程序在此过程中访问下一个节点。
- “归”表示函数返回,代表当前节点已经访问完毕。
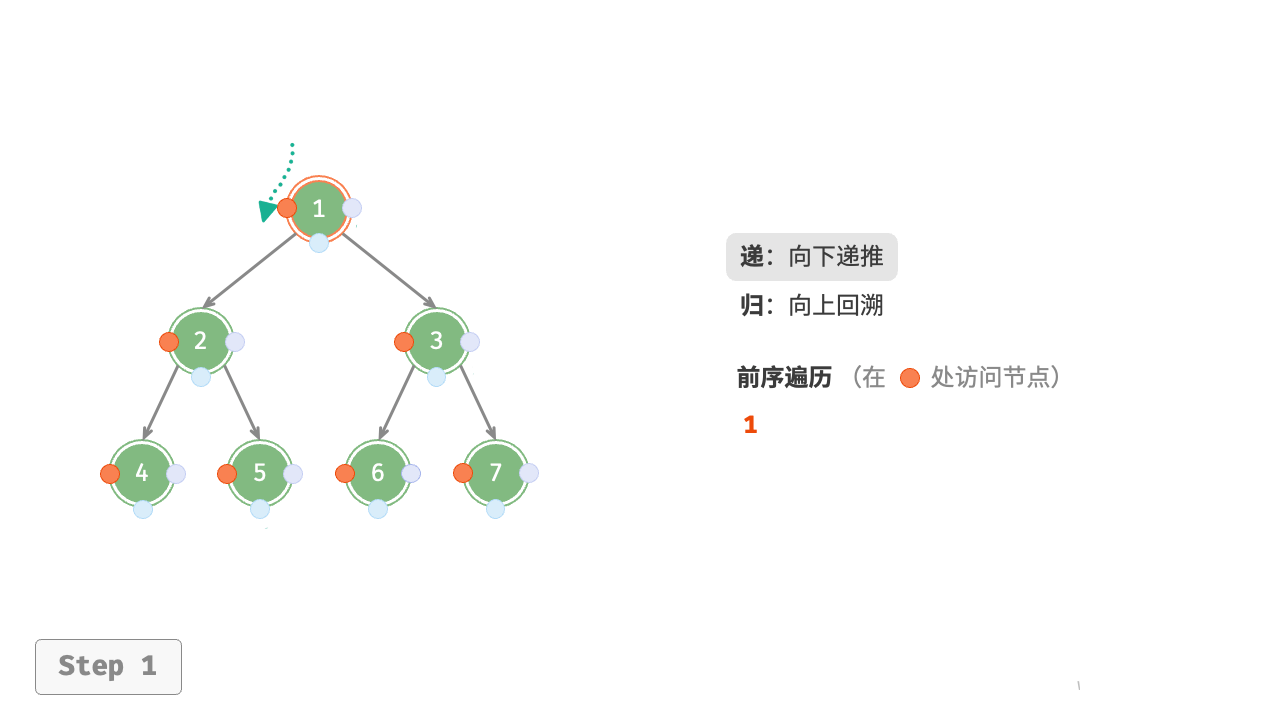
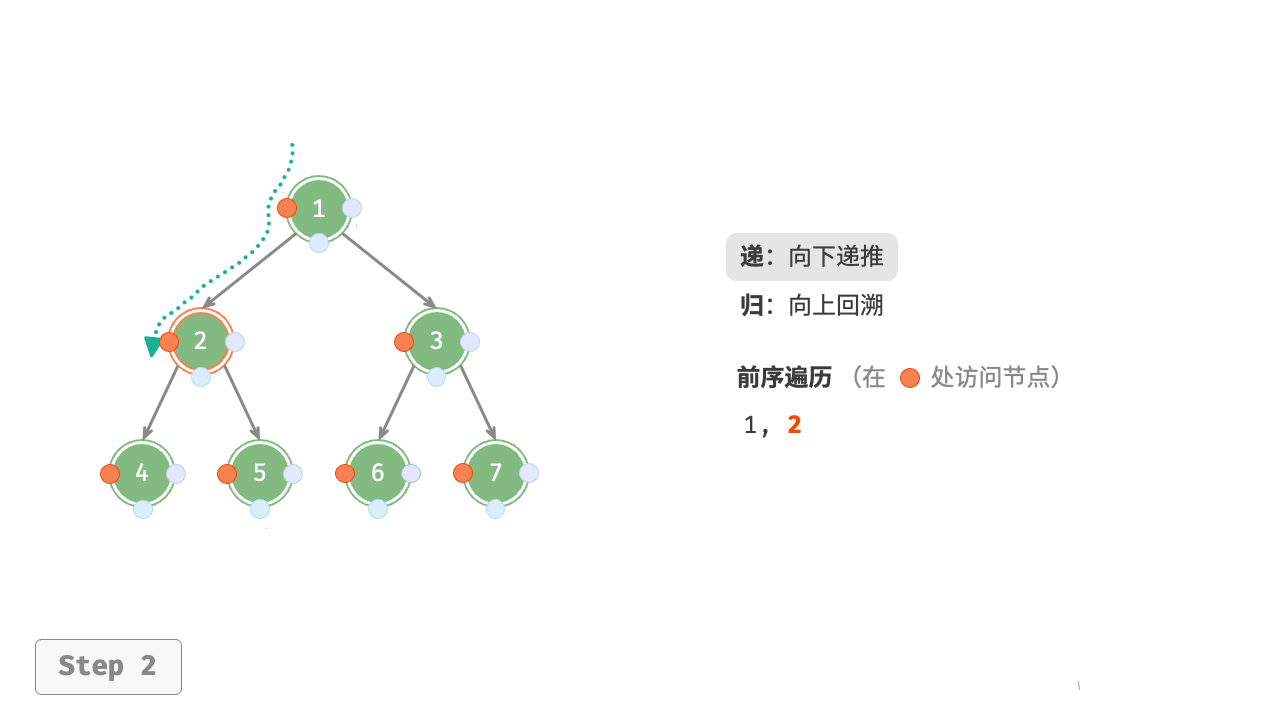
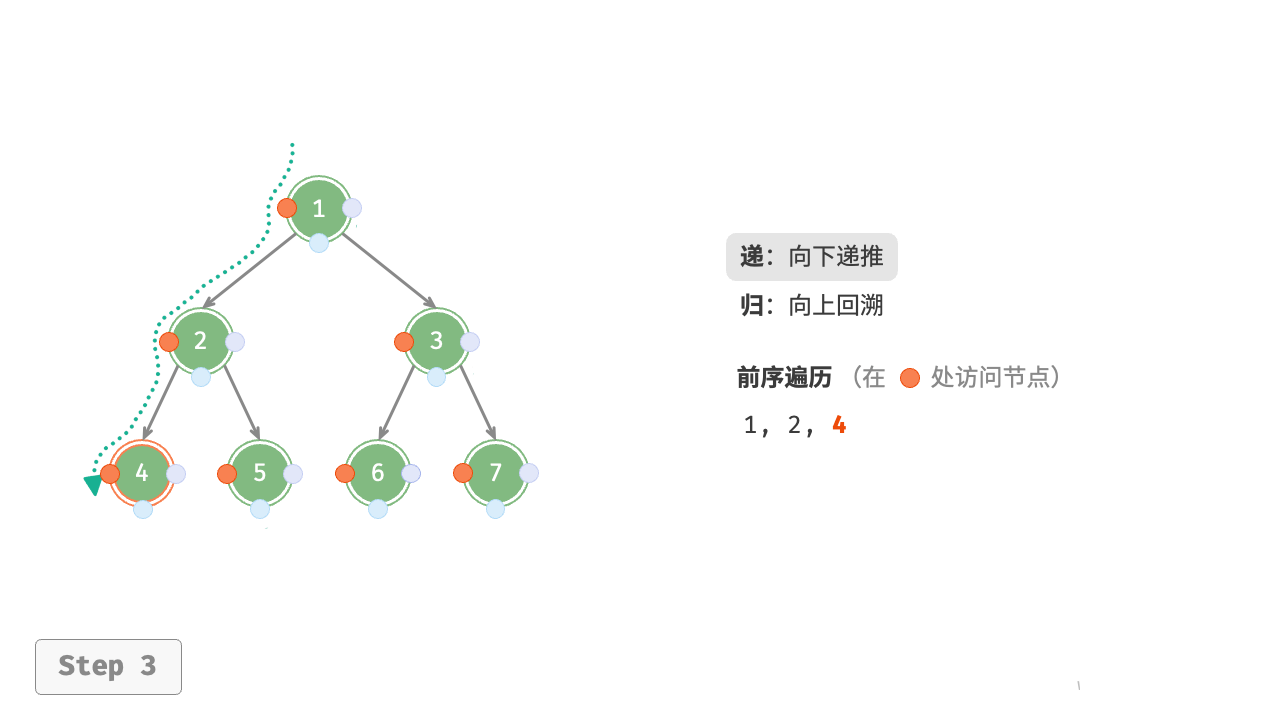
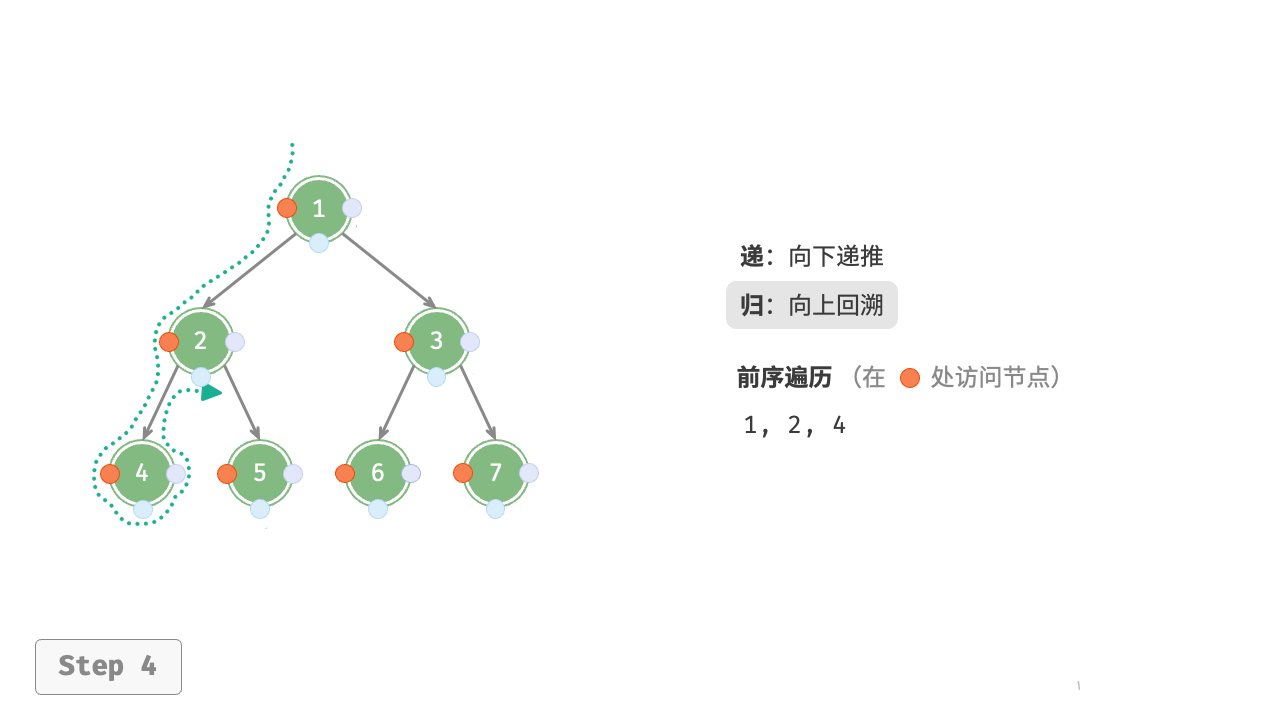
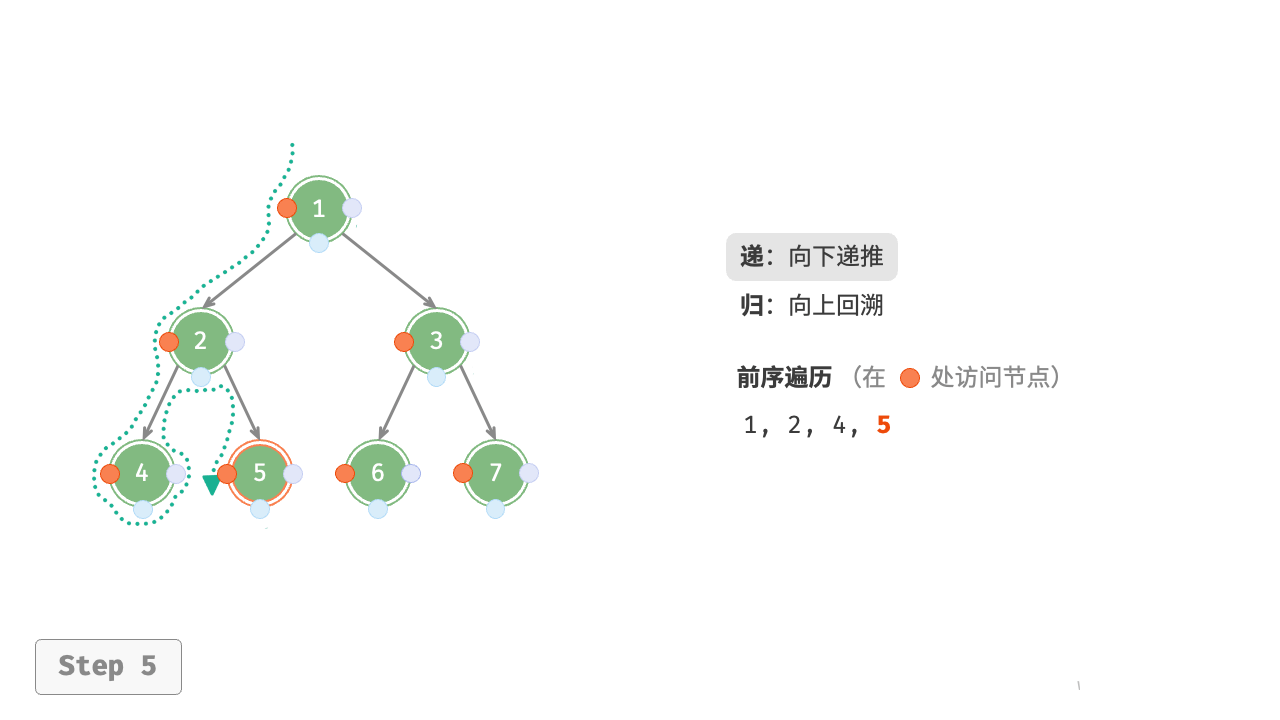
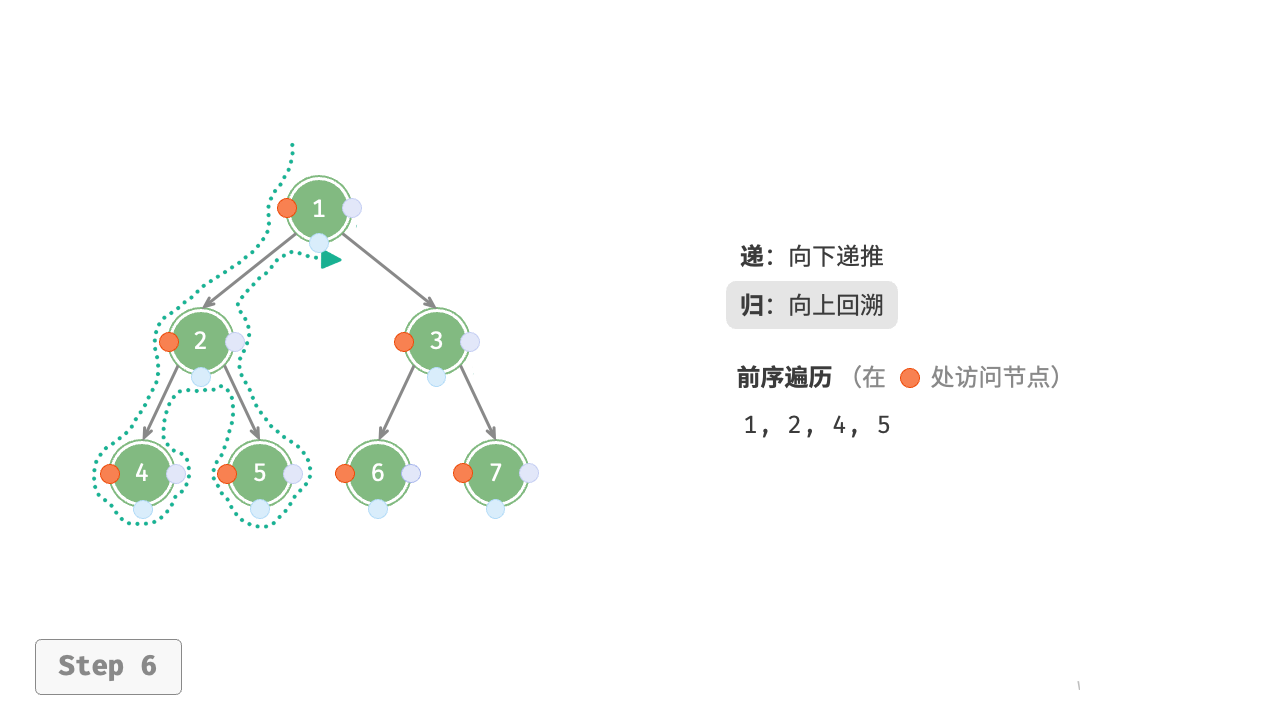
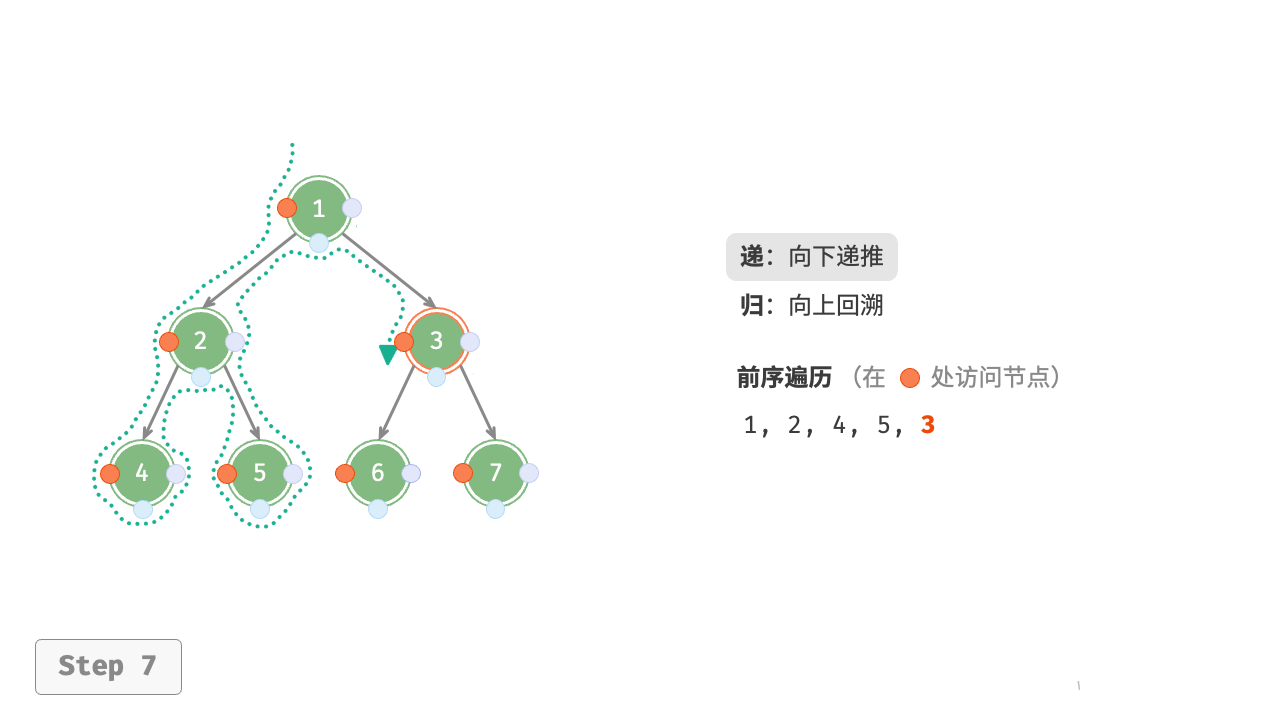
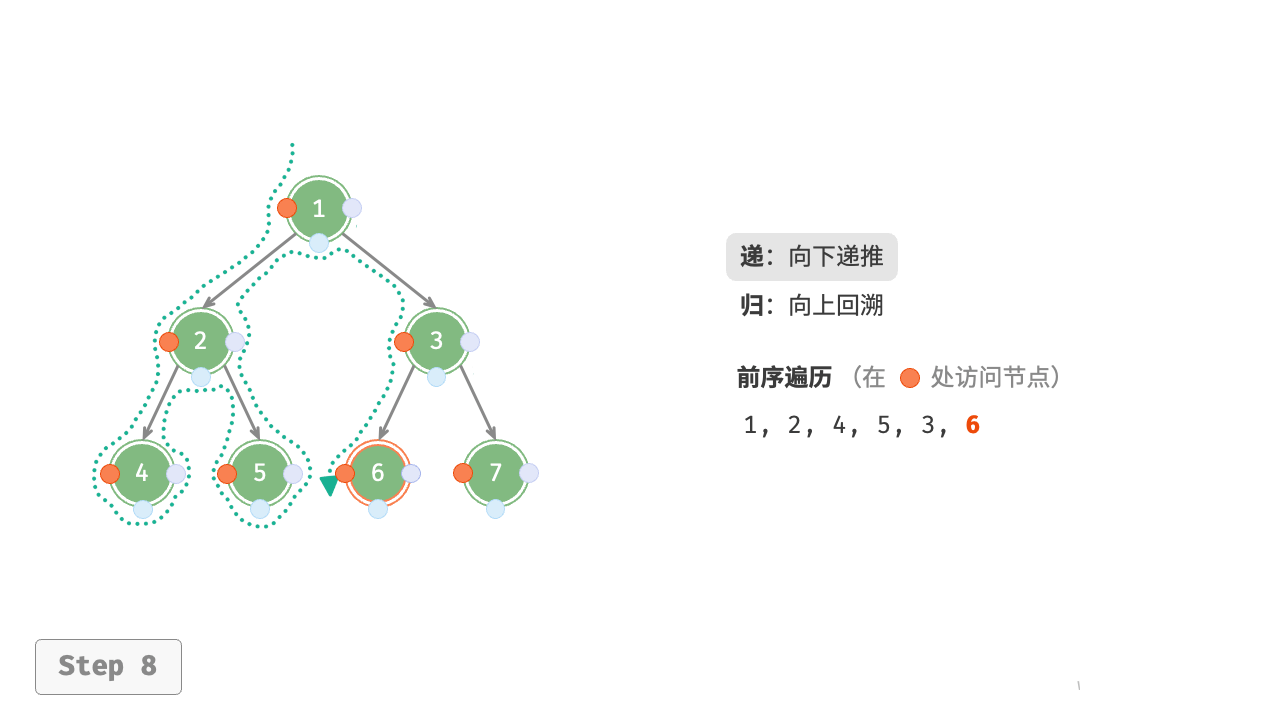
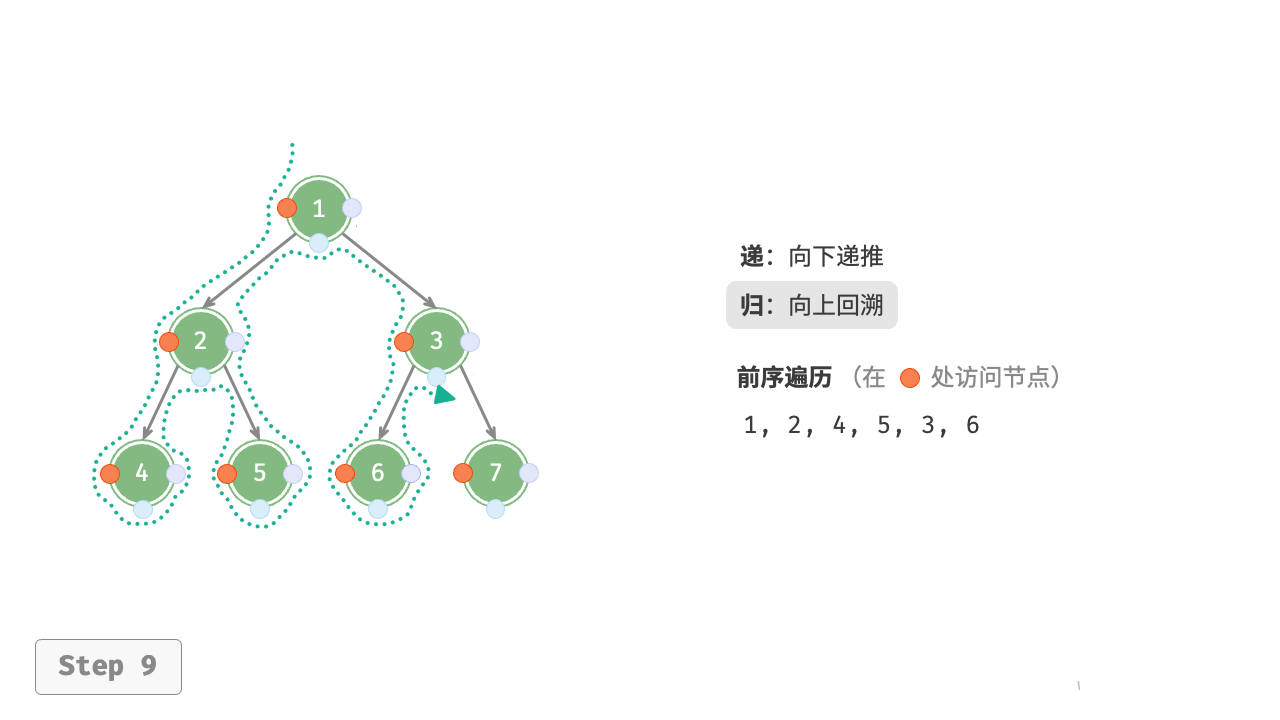
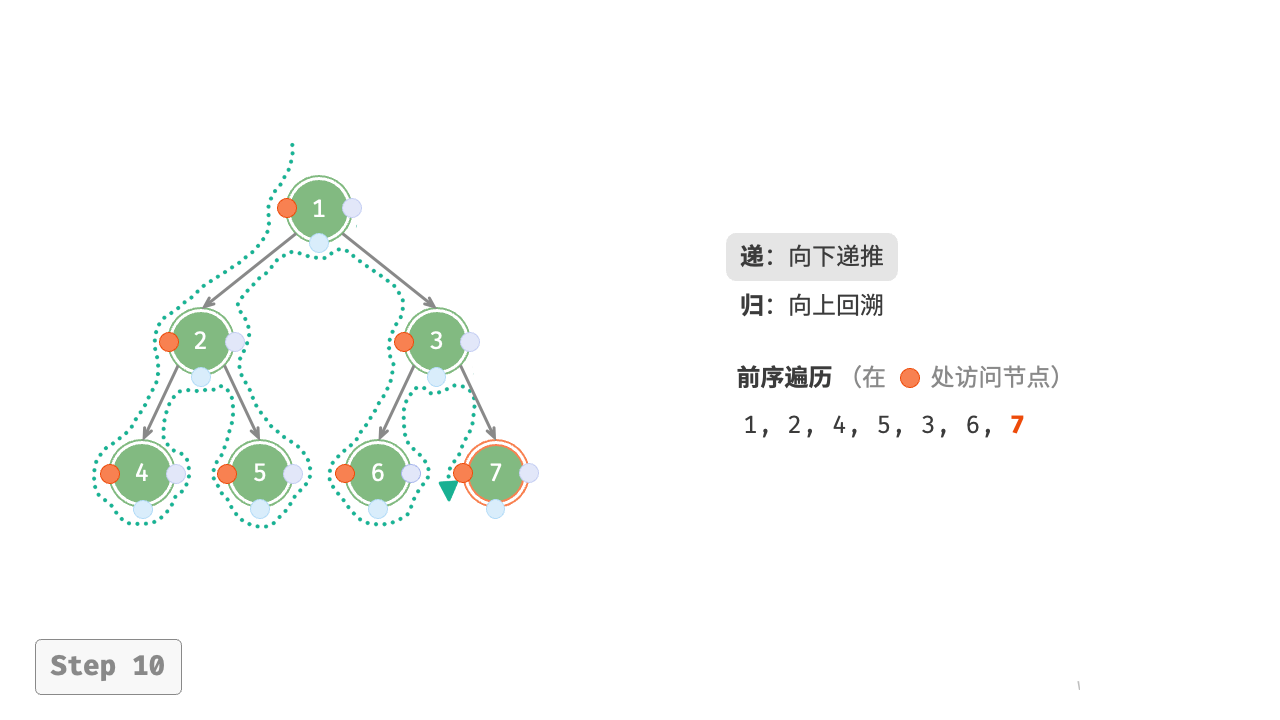
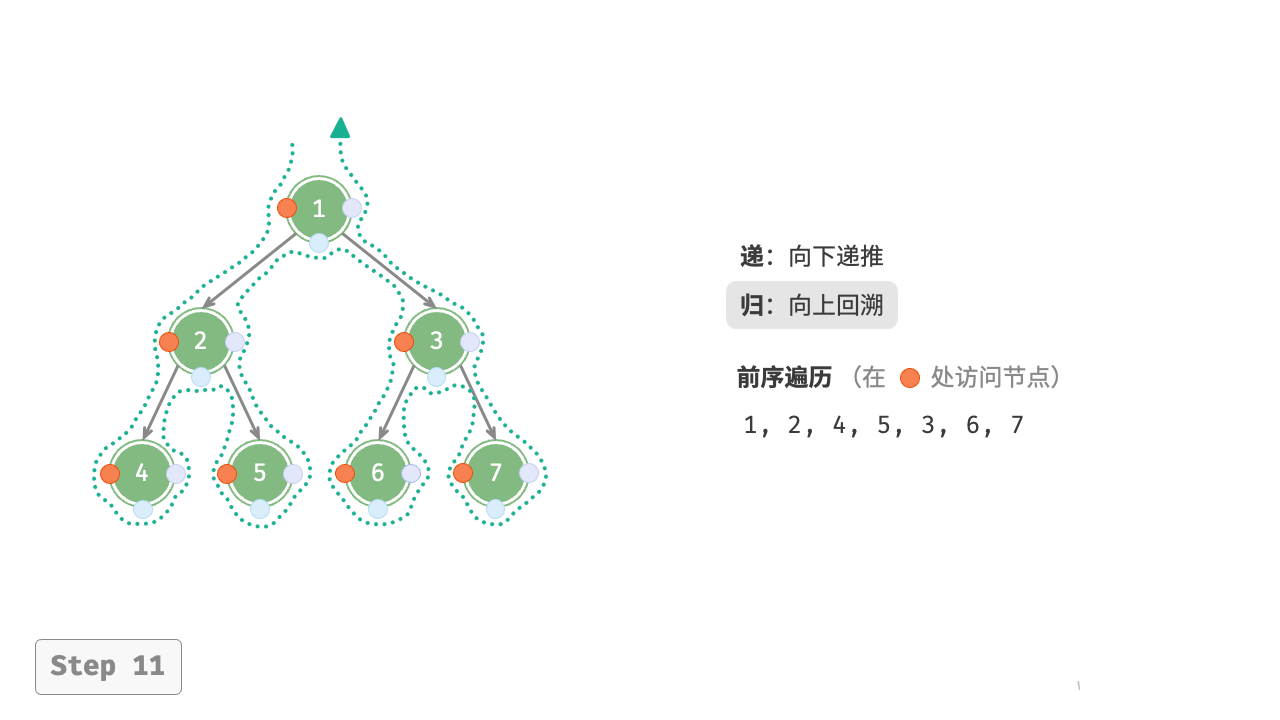
图 7-11 前序遍历的递归过程
6.2.2 复杂度分析
- 时间复杂度为 :所有节点被访问一次,使用 时间。
- 空间复杂度为 :在最差情况下,即树退化为链表时,递归深度达到 ,系统占用 栈帧空间。
7. 二叉树数组表示
在链表表示下,二叉树的存储单元为节点 TreeNode ,节点之间通过指针相连接。上一节介绍了链表表示下的二叉树的各项基本操作。
那么,我们能否用数组来表示二叉树呢?答案是肯定的。
7.1 表示完美二叉树
先分析一个简单案例。给定一棵完美二叉树,我们将所有节点按照层序遍历的顺序存储在一个数组中,则每个节点都对应唯一的数组索引。
根据层序遍历的特性,我们可以推导出父节点索引与子节点索引之间的“映射公式”:若某节点的索引为 ,则该节点的左子节点索引为 ,右子节点索引为 。图 7-12 展示了各个节点索引之间的映射关系。
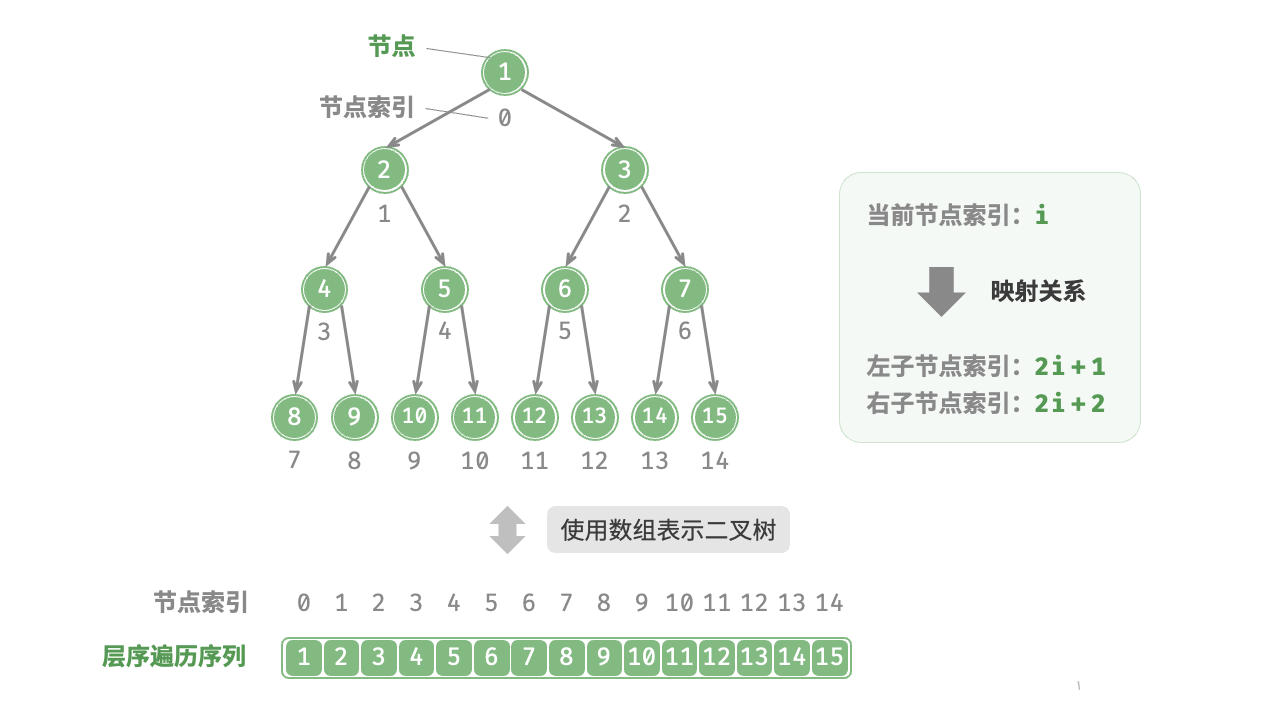
映射公式的角色相当于链表中的节点引用(指针)。给定数组中的任意一个节点,我们都可以通过映射公式来访问它的左(右)子节点。
7.2 表示任意二叉树
完美二叉树是一个特例,在二叉树的中间层通常存在许多 None 。由于层序遍历序列并不包含这些 None ,因此我们无法仅凭该序列来推测 None 的数量和分布位置。这意味着存在多种二叉树结构都符合该层序遍历序列。
如图 7-13 所示,给定一棵非完美二叉树,上述数组表示方法已经失效。
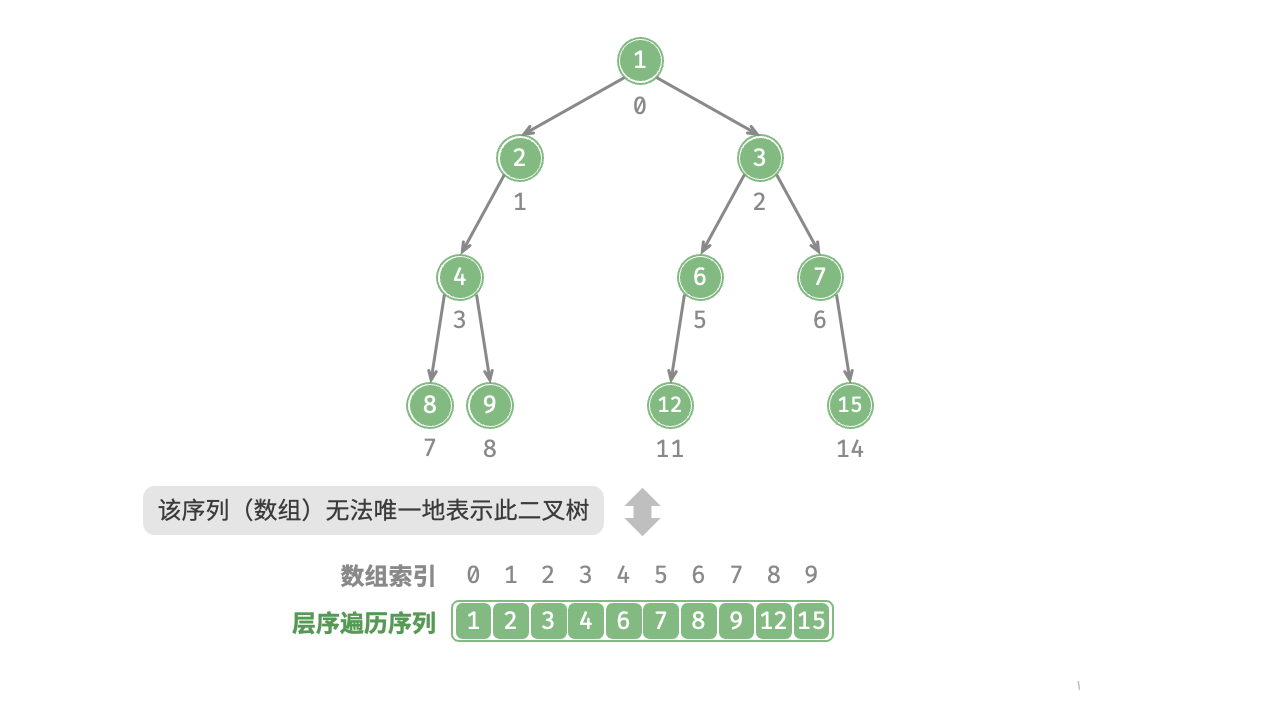
为了解决此问题,我们可以考虑在层序遍历序列中显式地写出所有 None 。如图 7-14 所示,这样处理后,层序遍历序列就可以唯一表示二叉树了。示例代码如下:
# 二叉树的数组表示
# 使用 None 来表示空位
tree = [1, 2, 3, 4, None, 6, 7, 8, 9, None, None, 12, None, None, 15]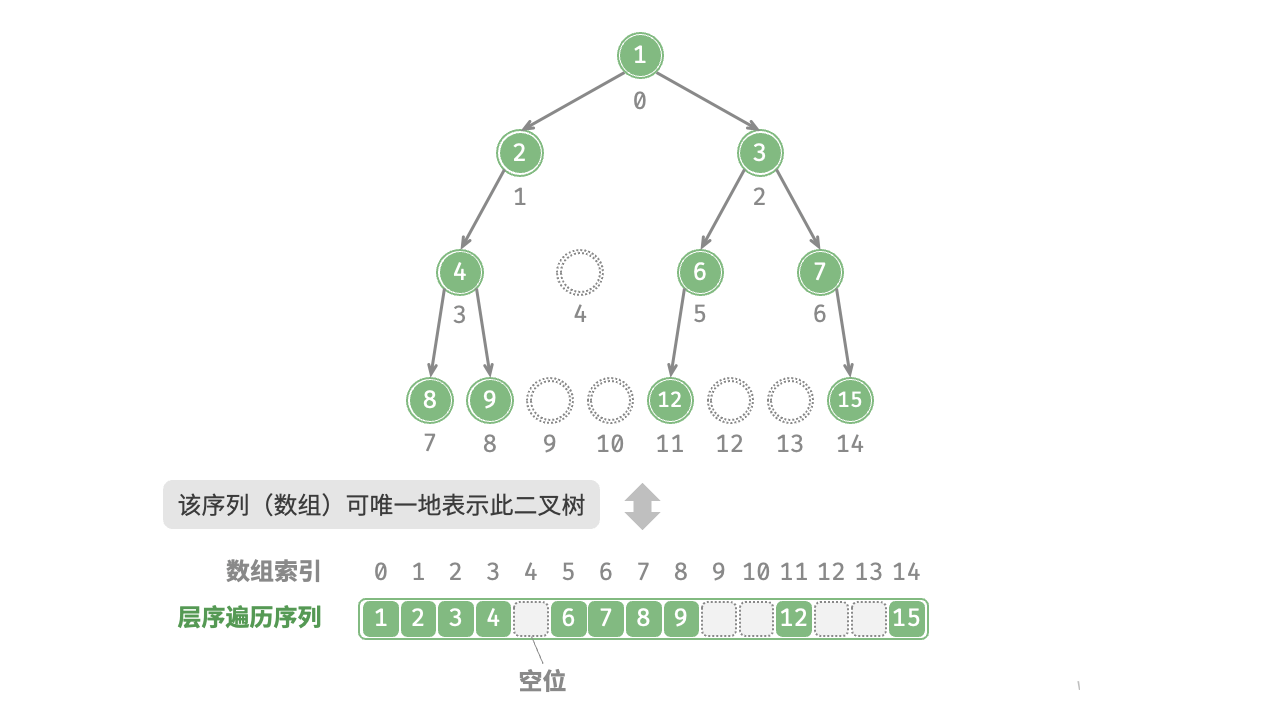
值得说明的是,完全二叉树非常适合使用数组来表示。回顾完全二叉树的定义,None 只出现在最底层且靠右的位置,因此所有 None 一定出现在层序遍历序列的末尾。
这意味着使用数组表示完全二叉树时,可以省略存储所有 None ,非常方便。图 7-15 给出了一个例子。
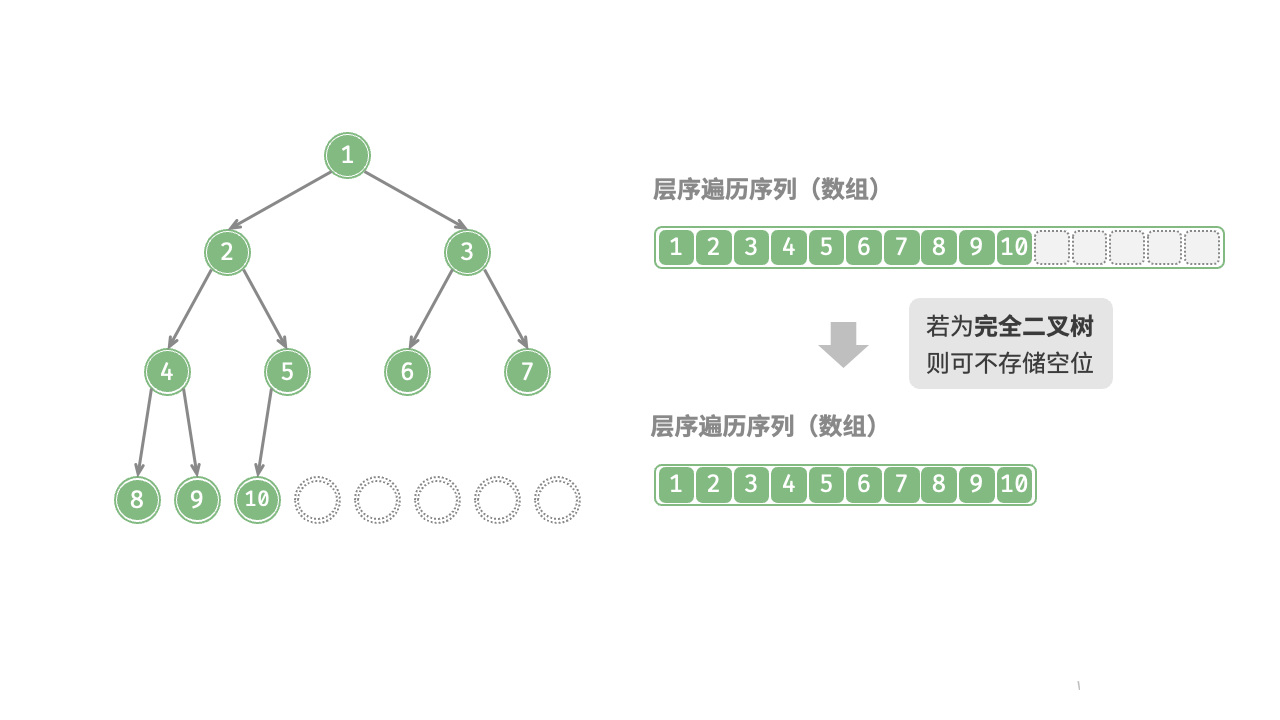
以下代码实现了一棵基于数组表示的二叉树,包括以下几种操作。
- 给定某节点,获取它的值、左(右)子节点、父节点。
- 获取前序遍历、中序遍历、后序遍历、层序遍历序列。
class ArrayBinaryTree:
"""数组表示下的二叉树类"""
def __init__(self, arr: list[int | None]):
"""构造方法"""
self._tree = list(arr)
def size(self):
"""列表容量"""
return len(self._tree)
def val(self, i: int) -> int | None:
"""获取索引为 i 节点的值"""
# 若索引越界,则返回 None ,代表空位
if i < 0 or i >= self.size():
return None
return self._tree[i]
def left(self, i: int) -> int | None:
"""获取索引为 i 节点的左子节点的索引"""
return 2 * i + 1
def right(self, i: int) -> int | None:
"""获取索引为 i 节点的右子节点的索引"""
return 2 * i + 2
def parent(self, i: int) -> int | None:
"""获取索引为 i 节点的父节点的索引"""
return (i - 1) // 2
def level_order(self) -> list[int]:
"""层序遍历"""
self.res = []
# 直接遍历数组
for i in range(self.size()):
if self.val(i) is not None:
self.res.append(self.val(i))
return self.res
def dfs(self, i: int, order: str):
"""深度优先遍历"""
if self.val(i) is None:
return
# 前序遍历
if order == "pre":
self.res.append(self.val(i))
self.dfs(self.left(i), order)
# 中序遍历
if order == "in":
self.res.append(self.val(i))
self.dfs(self.right(i), order)
# 后序遍历
if order == "post":
self.res.append(self.val(i))
def pre_order(self) -> list[int]:
"""前序遍历"""
self.res = []
self.dfs(0, order="pre")
return self.res
def in_order(self) -> list[int]:
"""中序遍历"""
self.res = []
self.dfs(0, order="in")
return self.res
def post_order(self) -> list[int]:
"""后序遍历"""
self.res = []
self.dfs(0, order="post")
return self.res7.3 优点与局限性
二叉树的数组表示主要有以下优点。
- 数组存储在连续的内存空间中,对缓存友好,访问与遍历速度较快。
- 不需要存储指针,比较节省空间。
- 允许随机访问节点。
然而,数组表示也存在一些局限性。
- 数组存储需要连续内存空间,因此不适合存储数据量过大的树。
- 增删节点需要通过数组插入与删除操作实现,效率较低。
- 当二叉树中存在大量
None时,数组中包含的节点数据比重较低,空间利用率较低。
8. 二叉搜索树
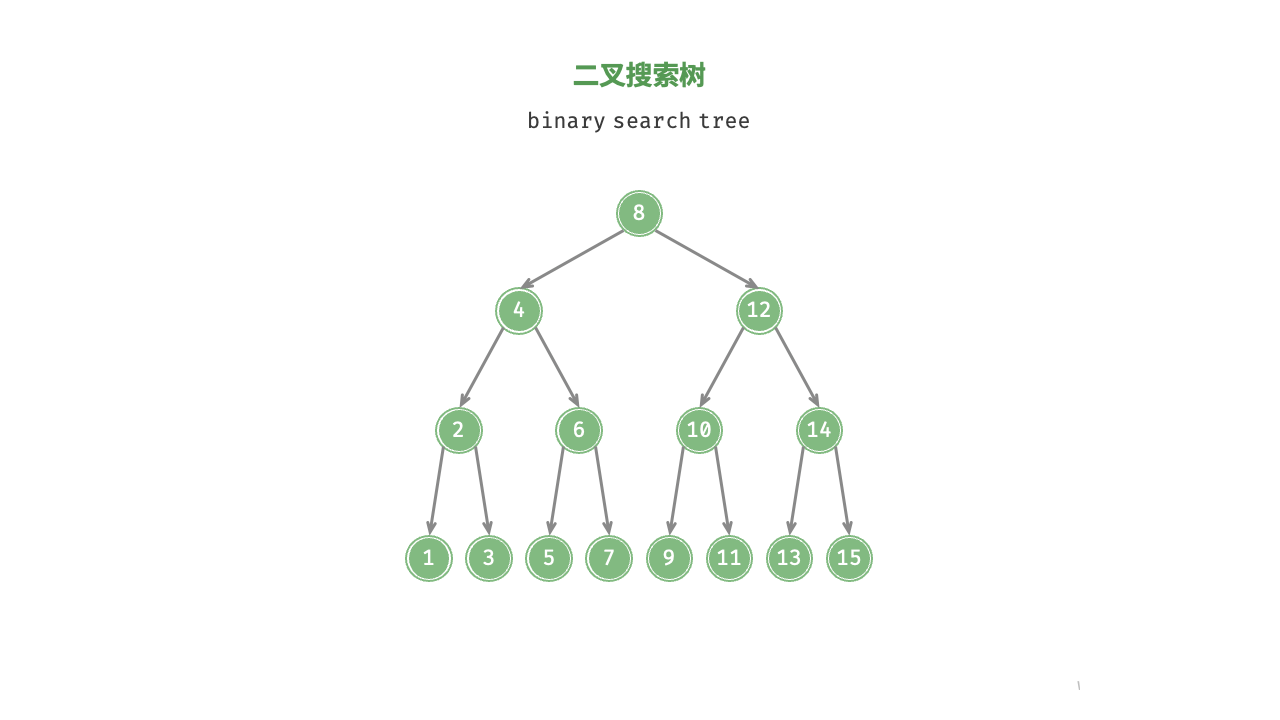
如图 7-16 所示,二叉搜索树(binary search tree)满足以下条件。
- 对于根节点,左子树中所有节点的值 < 根节点的值 < 右子树中所有节点的值。
- 任意节点的左、右子树也是二叉搜索树,即同样满足条件
1.。
8.1 二叉搜索树的操作
我们将二叉搜索树封装为一个类 BinarySearchTree ,并声明一个成员变量 root ,指向树的根节点。
8.1.1 查找节点
给定目标节点值 num ,可以根据二叉搜索树的性质来查找。如图 7-17 所示,我们声明一个节点 cur ,从二叉树的根节点 root 出发,循环比较节点值 cur.val 和 num 之间的大小关系。
- 若
cur.val < num,说明目标节点在cur的右子树中,因此执行cur = cur.right。 - 若
cur.val > num,说明目标节点在cur的左子树中,因此执行cur = cur.left。 - 若
cur.val = num,说明找到目标节点,跳出循环并返回该节点。
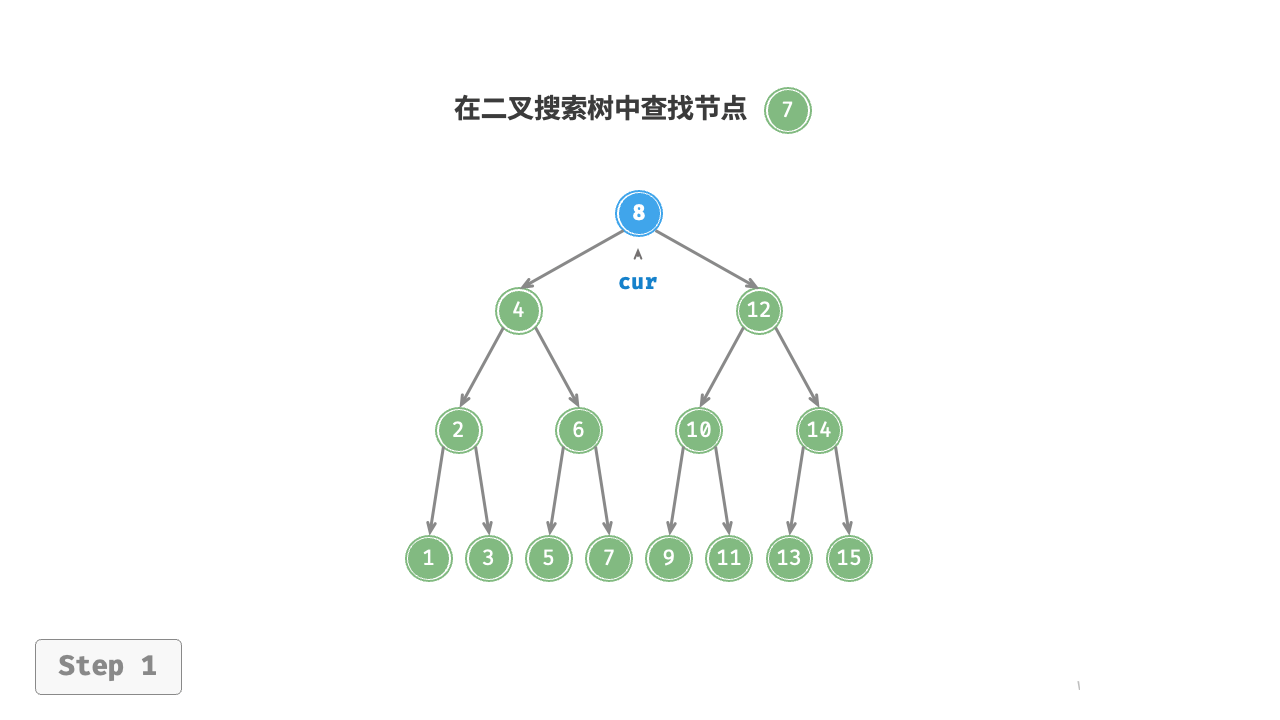
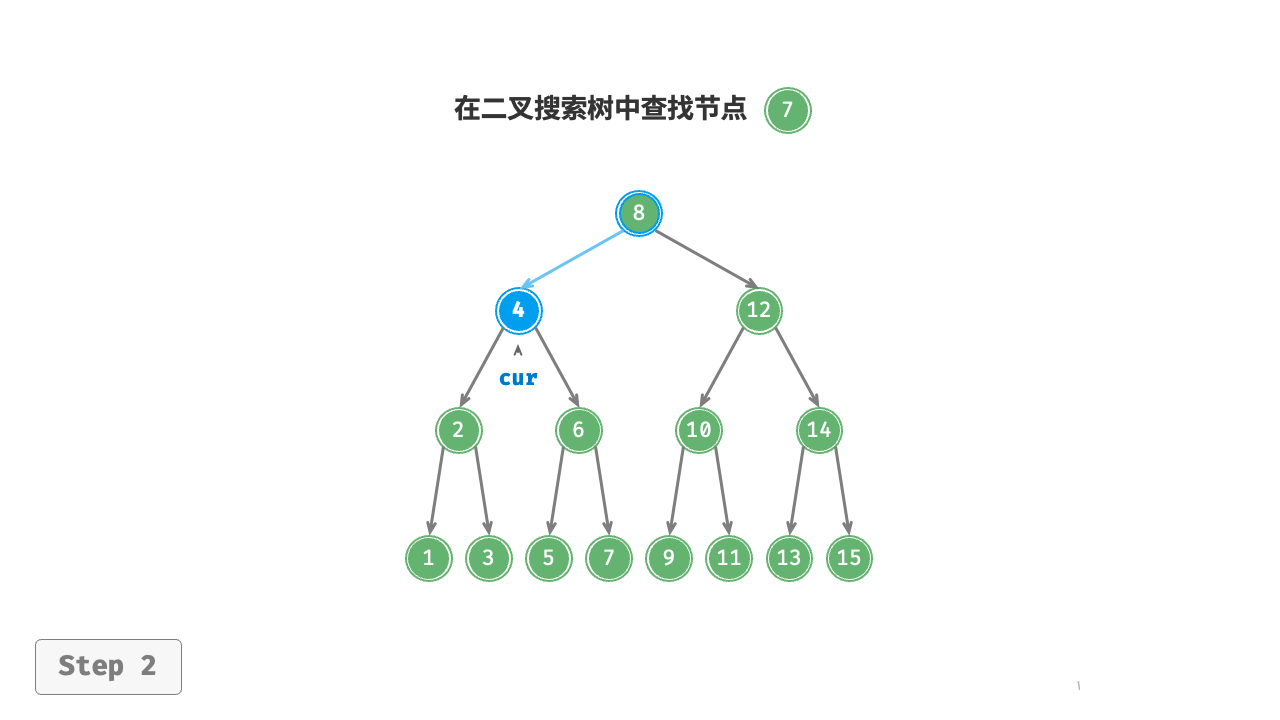
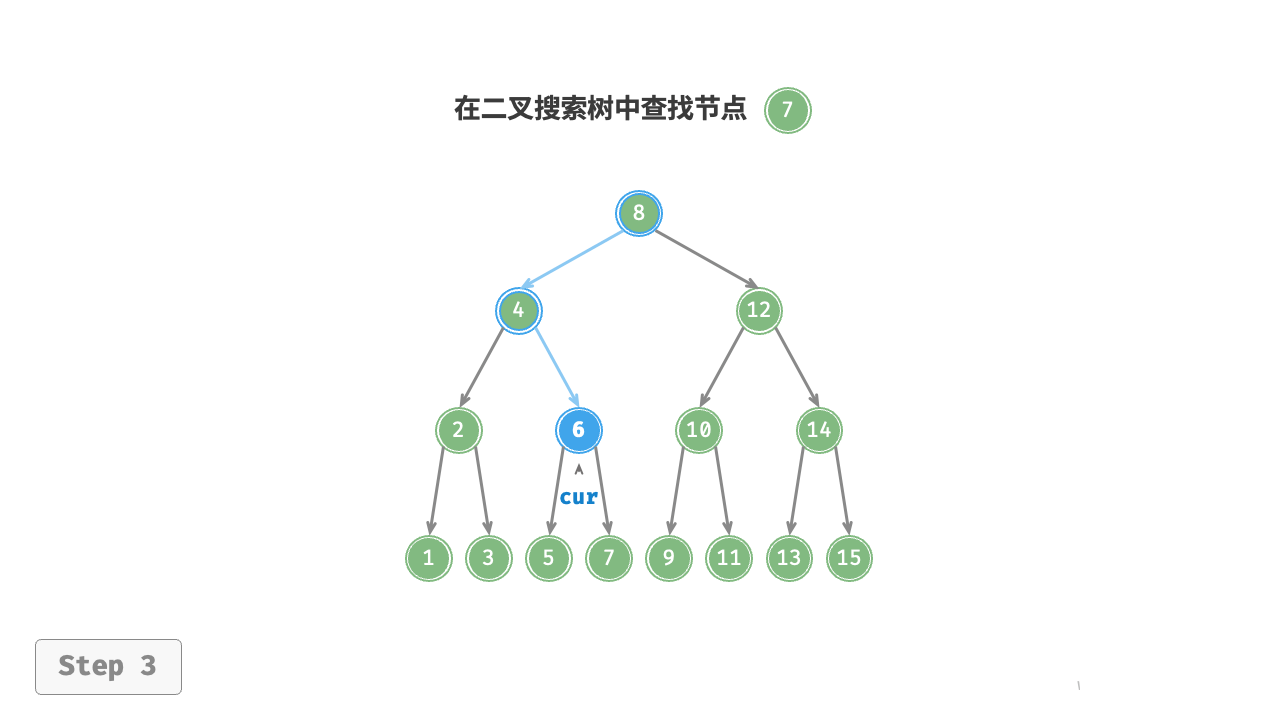
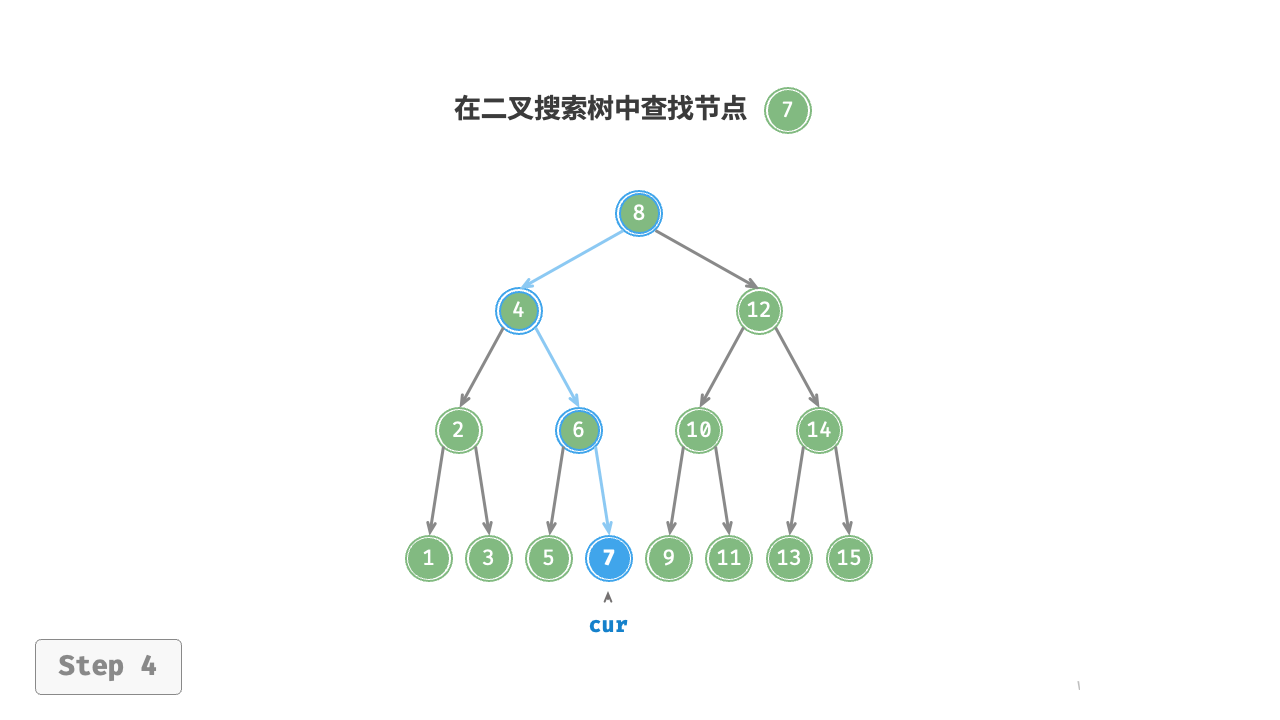
图 7-17 二叉搜索树查找节点示例
二叉搜索树的查找操作与二分查找算法的工作原理一致,都是每轮排除一半情况。循环次数最多为二叉树的高度,当二叉树平衡时,使用 时间。示例代码如下:
def search(self, num: int) -> TreeNode | None:
"""查找节点"""
cur = self._root
# 循环查找,越过叶节点后跳出
while cur is not None:
# 目标节点在 cur 的右子树中
if cur.val < num:
cur = cur.right
# 目标节点在 cur 的左子树中
elif cur.val > num:
cur = cur.left
# 找到目标节点,跳出循环
else:
break
return curclass TreeNode:
"""二叉树节点类"""
def __init__(self, val):
self.val = val
self.left = None
self.right = None
class BinarySearchTree:
"""二叉搜索树"""
def __init__(self):
"""构造方法"""
# 初始化空树
self._root = None
def search(self, num: int) -> TreeNode | None:
"""查找节点"""
cur = self._root
# 循环查找,越过叶节点后跳出
while cur is not None:
# 目标节点在 cur 的右子树中
if cur.val < num:
cur = cur.right
# 目标节点在 cur 的左子树中
elif cur.val > num:
cur = cur.left
# 找到目标节点,跳出循环
else:
break
return cur
def insert(self, num: int):
"""插入节点"""
# 若树为空,则初始化根节点
if self._root is None:
self._root = TreeNode(num)
return
# 循环查找,越过叶节点后跳出
cur, pre = self._root, None
while cur is not None:
# 找到重复节点,直接返回
if cur.val == num:
return
pre = cur
# 插入位置在 cur 的右子树中
if cur.val < num:
cur = cur.right
# 插入位置在 cur 的左子树中
else:
cur = cur.left
# 插入节点
node = TreeNode(num)
if pre.val < num:
pre.right = node
else:
pre.left = node
"""Driver Code"""
if __name__ == "__main__":
# 初始化二叉搜索树
bst = BinarySearchTree()
nums = [4, 2, 6, 1, 3, 5, 7]
for num in nums:
bst.insert(num)
# 查找节点
node = bst.search(7)
print("\n查找到的节点对象为: {},节点值 = {}".format(node, node.val))class TreeNode:
"""二叉树节点类"""
def __init__(self, val):
self.val = val
self.left = None
self.right = None
class BST:
def __init__(self):
self.root = None
def search(self, root, val):
if root is None:
return None
if val < root.val:
return self.search(root.left, val)
elif val > root.val:
return self.search(root.right, val)
else:
return root
if __name__ == '__main__':
# 手动创建二叉搜索树
bst = BST()
bst.root = TreeNode(4)
bst.root.left = TreeNode(2)
bst.root.right = TreeNode(6)
bst.root.left.left = TreeNode(1)
bst.root.left.right = TreeNode(3)
bst.root.right.left = TreeNode(5)
bst.root.right.right = TreeNode(7)
# 测试查找节点
node = bst.search(bst.root, 7)
if node:
print(f"找到了节点,值为: {node.val}")
else:
print("未找到节点")class TreeNode:
"""二叉树节点类"""
def __init__(self, val):
self.val = val
self.left = None
self.right = None
class BST:
def __init__(self):
self.root = None
def search(self, root, val):
"""搜索二叉搜索树中的值"""
if root is None:
return None
if val < root.val:
return self.search(root.left, val)
elif val > root.val:
return self.search(root.right, val)
else:
return root # 找到匹配节点
if __name__ == '__main__':
# 手动创建二叉搜索树
bst = BST()
bst.root = TreeNode(4)
bst.root.left = TreeNode(2)
bst.root.right = TreeNode(6)
bst.root.left.left = TreeNode(1)
bst.root.left.right = TreeNode(3)
bst.root.right.left = TreeNode(5)
bst.root.right.right = TreeNode(7)
# 测试查找节点
node = bst.search(bst.root, 7)
if node:
print(f"找到了节点,值为: {node.val}")
else:
print("未找到节点")8.1.2 插入节点
给定一个待插入元素 num ,为了保持二叉搜索树“左子树 < 根节点 < 右子树”的性质,插入操作流程如图 7-18 所示。
- 查找插入位置:与查找操作相似,从根节点出发,根据当前节点值和
num的大小关系循环向下搜索,直到越过叶节点(遍历至None)时跳出循环。 - 在该位置插入节点:初始化节点
num,将该节点置于None的位置。
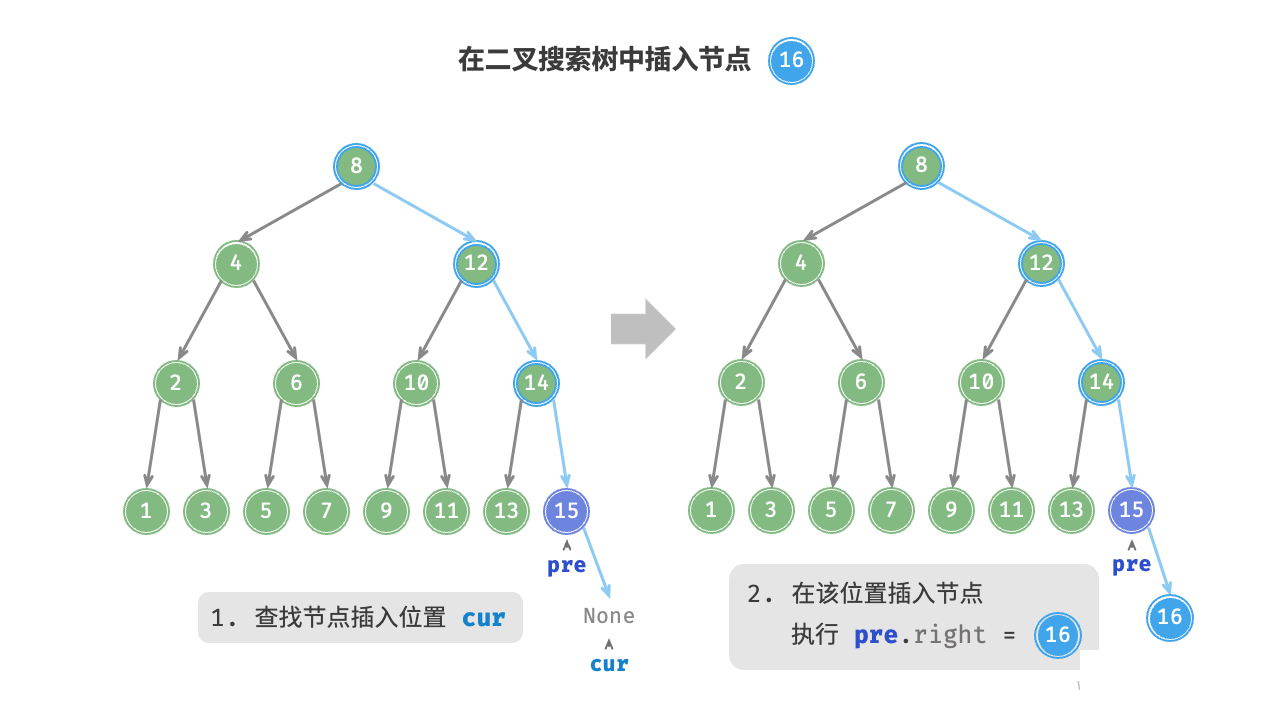
在代码实现中,需要注意以下两点。
- 二叉搜索树不允许存在重复节点,否则将违反其定义。因此,若待插入节点在树中已存在,则不执行插入,直接返回。
- 为了实现插入节点,我们需要借助节点
pre保存上一轮循环的节点。这样在遍历至None时,我们可以获取到其父节点,从而完成节点插入操作。
def insert(self, num: int):
"""插入节点"""
# 若树为空,则初始化根节点
if self._root is None:
self._root = TreeNode(num)
return
# 循环查找,越过叶节点后跳出
cur, pre = self._root, None
while cur is not None:
# 找到重复节点,直接返回
if cur.val == num:
return
pre = cur
# 插入位置在 cur 的右子树中
if cur.val < num:
cur = cur.right
# 插入位置在 cur 的左子树中
else:
cur = cur.left
# 插入节点
node = TreeNode(num)
if pre.val < num:
pre.right = node
else:
pre.left = nodeclass TreeNode:
"""二叉树节点类"""
def __init__(self, val):
self.val = val
self.left = None
self.right = None
class BinarySearchTree:
"""二叉搜索树"""
def __init__(self):
"""构造方法"""
# 初始化空树
self._root = None
def insert(self, num: int):
"""插入节点"""
# 若树为空,则初始化根节点
if self._root is None:
self._root = TreeNode(num)
return
# 循环查找,越过叶节点后跳出
cur, pre = self._root, None
while cur is not None:
# 找到重复节点,直接返回
if cur.val == num:
return
pre = cur
# 插入位置在 cur 的右子树中
if cur.val < num:
cur = cur.right
# 插入位置在 cur 的左子树中
else:
cur = cur.left
# 插入节点
node = TreeNode(num)
if pre.val < num:
pre.right = node
else:
pre.left = node
"""Driver Code"""
if __name__ == "__main__":
# 初始化二叉搜索树
bst = BinarySearchTree()
nums = [4, 2, 6, 1, 3, 5, 7]
for num in nums:
bst.insert(num)
# 插入节点
bst.insert(16)class TreeNode:
"""二叉树节点类"""
def __init__(self, val):
self.val = val
self.left = None
self.right = None
class BST:
def __init__(self):
self.root = None
def search(self, root, val):
if root is None:
return None
if val < root.val:
return self.search(root.left, val)
elif val > root.val:
return self.search(root.right, val)
else:
return root
def insert(self, root, num):
if root is None:
return TreeNode(num) # 返回新创建的节点
if num < root.val:
root.left = self.insert(root.left, num) # 更新左子节点
elif num > root.val:
root.right = self.insert(root.right, num) # 更新右子节点
return root
if __name__ == '__main__':
# 创建一个空的二叉搜索树
bst = BST()
# 通过 insert 方法插入所有节点
bst.root = bst.insert(bst.root, 4)
bst.insert(bst.root, 2)
bst.insert(bst.root, 6)
bst.insert(bst.root, 1)
bst.insert(bst.root, 3)
bst.insert(bst.root, 5)
bst.insert(bst.root, 7)
# 测试查找节点
node = bst.search(bst.root, 7)
if node:
print(f"找到了节点,值为: {node.val}")
else:
print("未找到节点")
# 测试插入新节点
bst.insert(bst.root, 8)
node = bst.search(bst.root, 8)
if node:
print(f"找到了节点,值为: {node.val}")
else:
print("未找到节点")与查找节点相同,插入节点使用 时间。
8.1.3 删除节点
先在二叉树中查找到目标节点,再将其删除。与插入节点类似,我们需要保证在删除操作完成后,二叉搜索树的“左子树 < 根节点 < 右子树”的性质仍然满足。因此,我们根据目标节点的子节点数量,分 0、1 和 2 三种情况,执行对应的删除节点操作。
如图 7-19 所示,当待删除节点的度为 时,表示该节点是叶节点,可以直接删除。
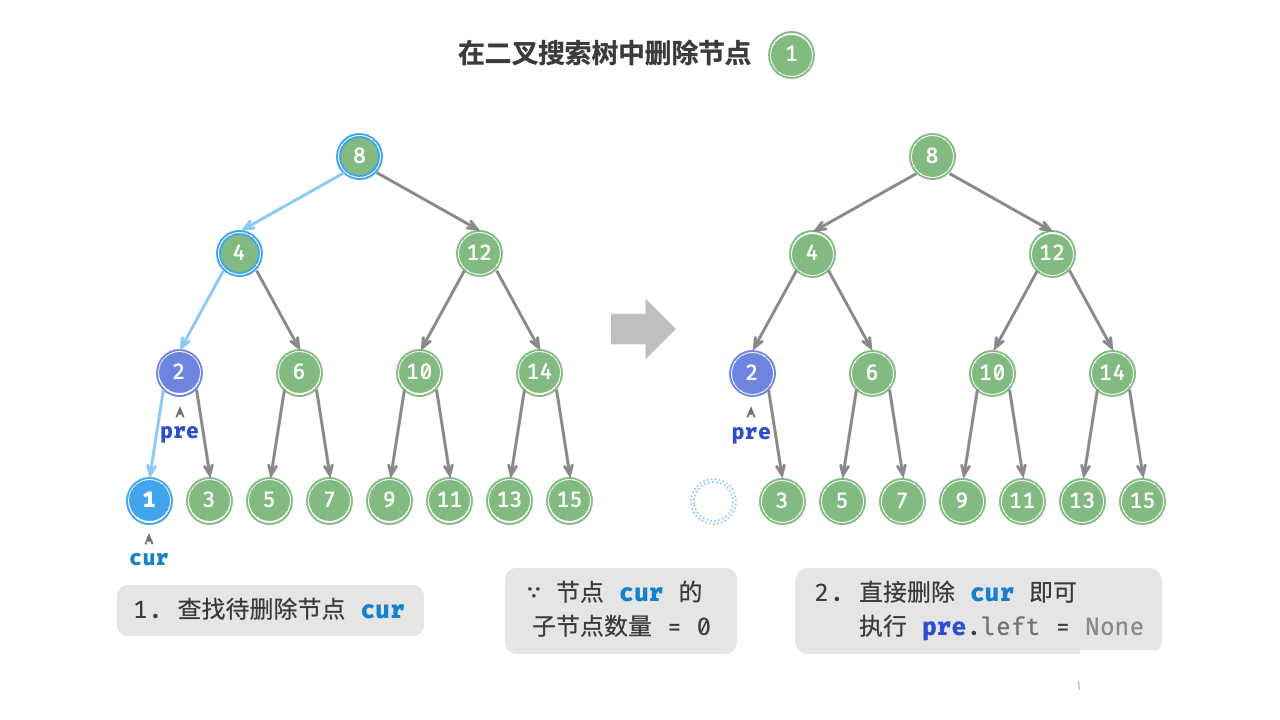
如图 7-20 所示,当待删除节点的度为 时,将待删除节点替换为其子节点即可。
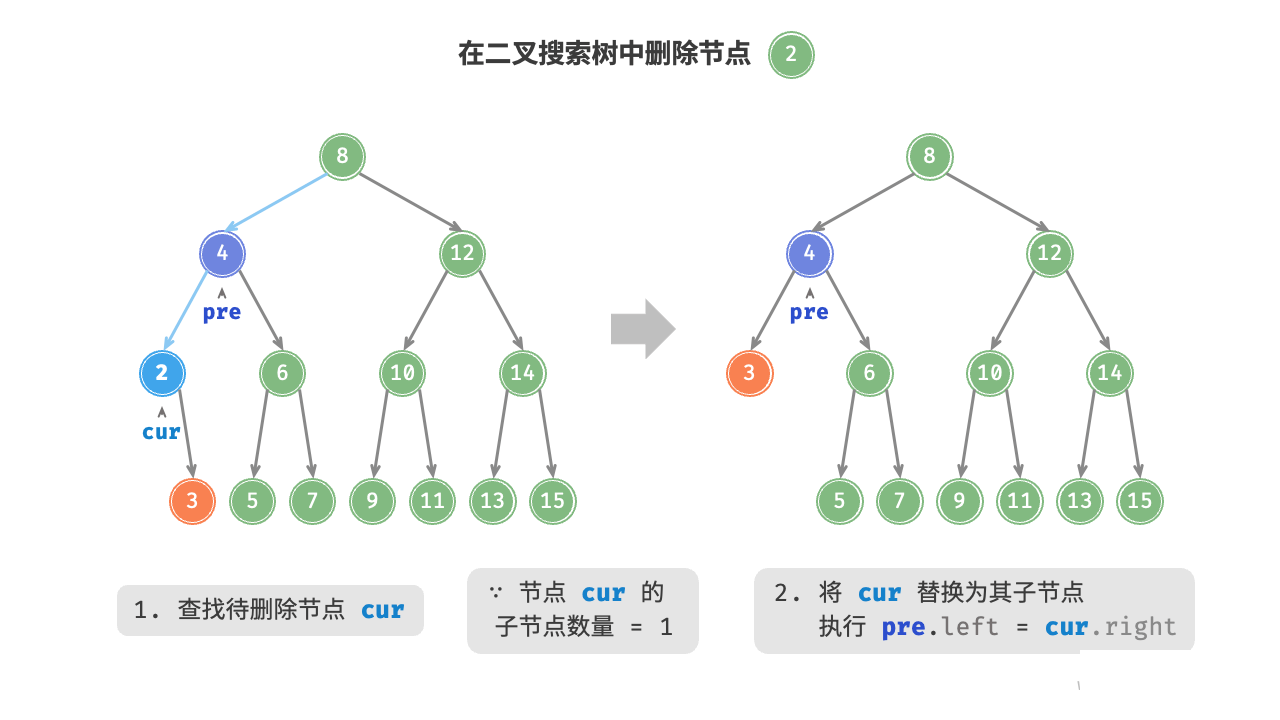
当待删除节点的度为 2 时,我们无法直接删除它,而需要使用一个节点替换该节点。由于要保持二叉搜索树“左子树 根节点 右子树”的性质,因此这个节点可以是右子树的最小节点或左子树的最大节点。
假设我们选择右子树的最小节点(中序遍历的下一个节点),则删除操作流程如图 7-21 所示。
- 找到待删除节点在“中序遍历序列”中的下一个节点,记为
tmp。 - 用
tmp的值覆盖待删除节点的值,并在树中递归删除节点tmp。
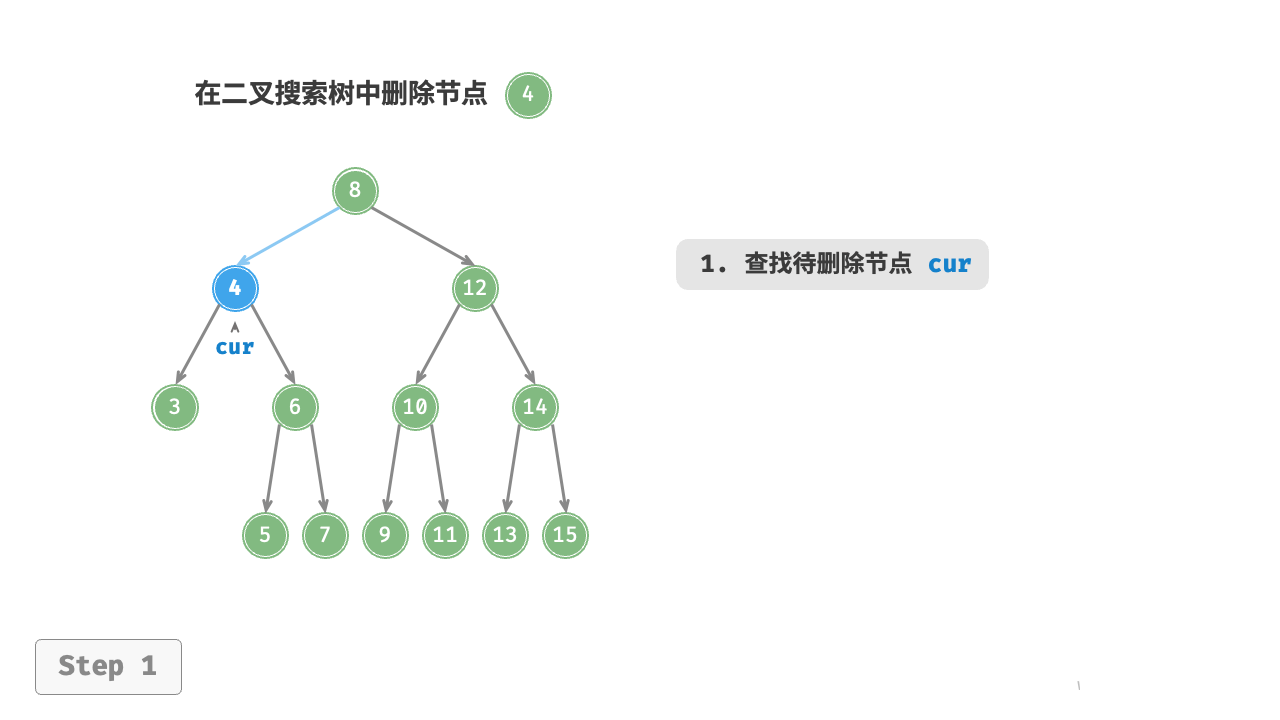
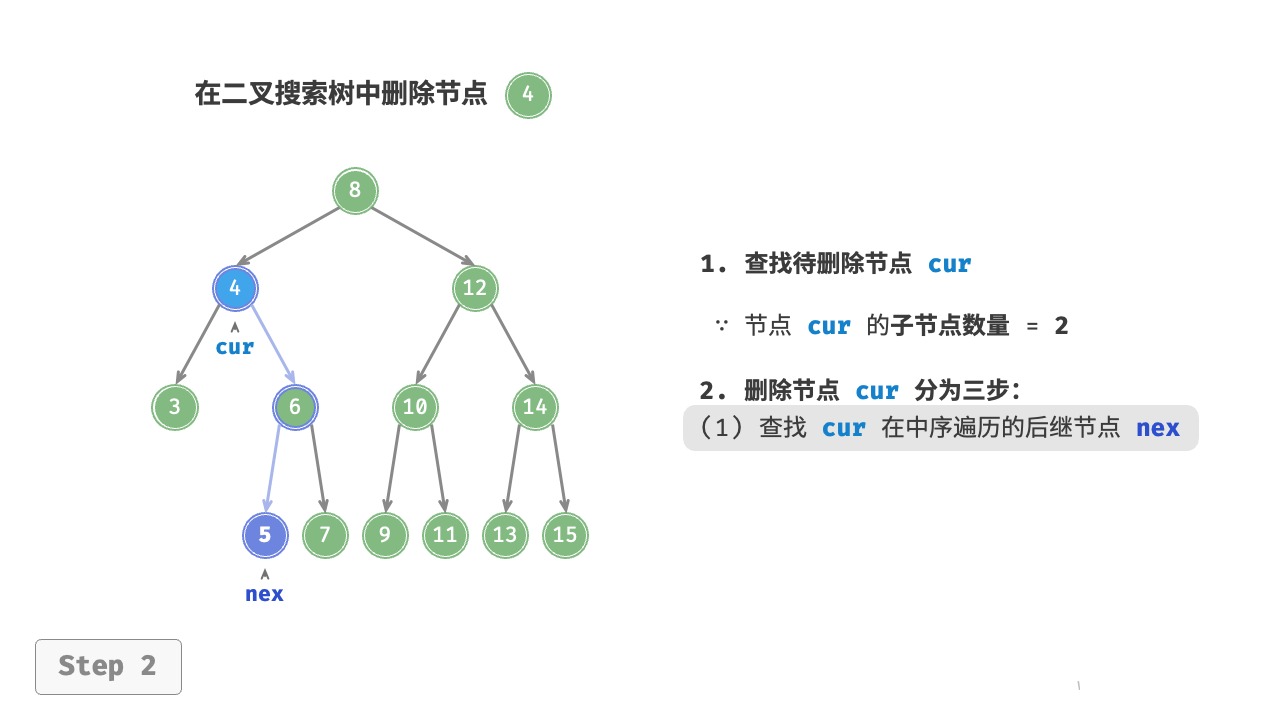

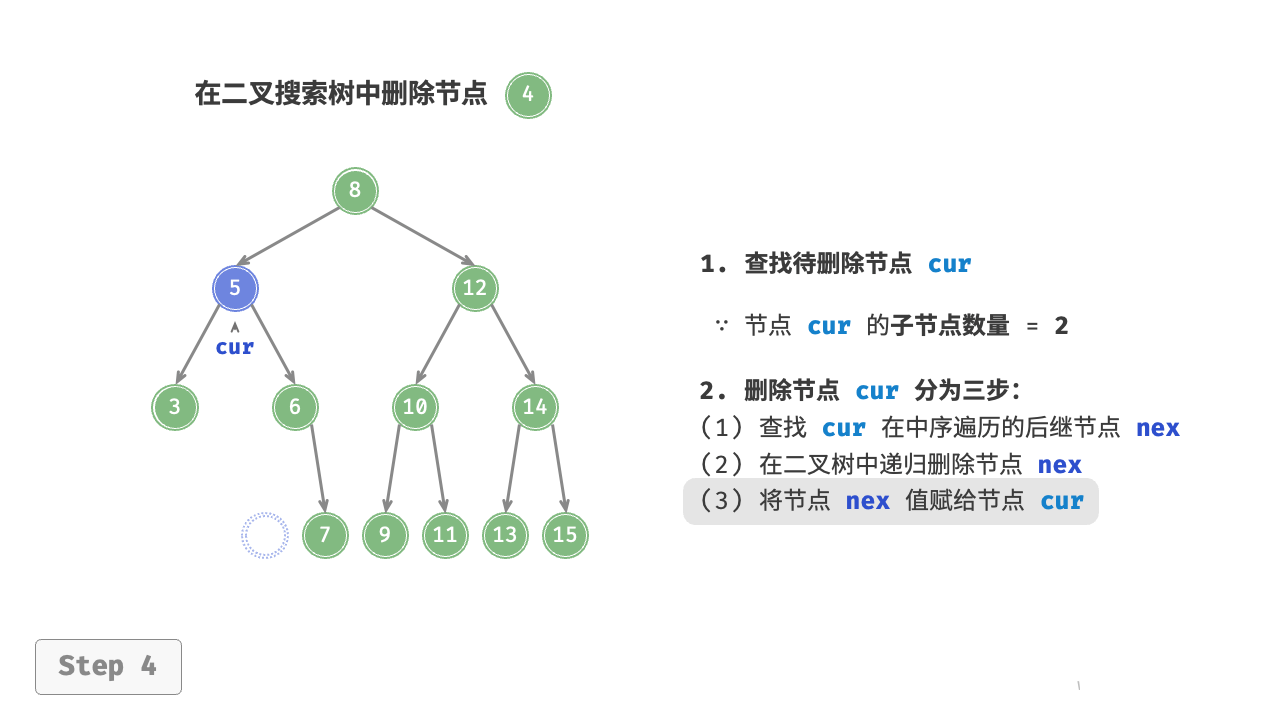
图 7-21 在二叉搜索树中删除节点(度为 )
删除节点操作同样使用 时间,其中查找待删除节点需要 时间,获取中序遍历后继节点需要 时间。示例代码如下:
def remove(self, num: int):
"""删除节点"""
# 若树为空,直接提前返回
if self._root is None:
return
# 循环查找,越过叶节点后跳出
cur, pre = self._root, None
while cur is not None:
# 找到待删除节点,跳出循环
if cur.val == num:
break
pre = cur
# 待删除节点在 cur 的右子树中
if cur.val < num:
cur = cur.right
# 待删除节点在 cur 的左子树中
else:
cur = cur.left
# 若无待删除节点,则直接返回
if cur is None:
return
# 子节点数量 = 0 or 1
if cur.left is None or cur.right is None:
# 当子节点数量 = 0 / 1 时, child = null / 该子节点
child = cur.left or cur.right
# 删除节点 cur
if cur != self._root:
if pre.left == cur:
pre.left = child
else:
pre.right = child
else:
# 若删除节点为根节点,则重新指定根节点
self._root = child
# 子节点数量 = 2
else:
# 获取中序遍历中 cur 的下一个节点
tmp: TreeNode = cur.right
while tmp.left is not None:
tmp = tmp.left
# 递归删除节点 tmp
self.remove(tmp.val)
# 用 tmp 覆盖 cur
cur.val = tmp.valclass TreeNode:
"""二叉树节点类"""
def __init__(self, val):
self.val = val
self.left = None
self.right = None
class BinarySearchTree:
"""二叉搜索树"""
def __init__(self):
"""构造方法"""
self._root = None
def insert(self, num: int):
"""插入节点"""
if self._root is None:
self._root = TreeNode(num)
return
cur, pre = self._root, None
while cur is not None:
if cur.val == num:
return
pre = cur
if cur.val < num:
cur = cur.right
else:
cur = cur.left
node = TreeNode(num)
if pre.val < num:
pre.right = node
else:
pre.left = node
def remove(self, num: int):
"""删除节点"""
if self._root is None:
return
# 查找节点
cur, pre = self._root, None
while cur is not None:
if cur.val == num:
break
pre = cur
if cur.val < num:
cur = cur.right
else:
cur = cur.left
if cur is None:
return
# 子节点数量 = 0 or 1
if cur.left is None or cur.right is None:
# 当子节点数量 = 0 / 1 时, child = null / 该子节点
child = cur.left or cur.right
# 删除节点 cur
if cur != self._root:
if pre.left == cur:
pre.left = child
else:
pre.right = child
else:
self._root = child
# 子节点数量 = 2
else:
# 获取中序遍历中 cur 的下一个节点
tmp: TreeNode = cur.right
while tmp.left is not None:
tmp = tmp.left
# 递归删除节点 tmp
self.remove(tmp.val)
# 用 tmp 覆盖 cur
cur.val = tmp.val
"""Driver Code"""
if __name__ == "__main__":
# 初始化二叉搜索树
bst = BinarySearchTree()
nums = [4, 2, 6, 1, 3, 5, 7]
for num in nums:
bst.insert(num)
# 删除节点
bst.remove(1) # 度为 0
bst.remove(2) # 度为 1
bst.remove(4) # 度为 2class TreeNode:
"""二叉树节点类"""
def __init__(self, val):
self.val = val
self.left = None
self.right = None
class BinarySearchTree:
"""二叉搜索树"""
def __init__(self):
"""构造方法"""
self._root = None
def insert(self, num: int):
"""插入节点"""
if self._root is None:
self._root = TreeNode(num)
return
cur, pre = self._root, None
while cur is not None:
if cur.val == num:
return
pre = cur
if cur.val < num:
cur = cur.right
else:
cur = cur.left
node = TreeNode(num)
if pre.val < num:
pre.right = node
else:
pre.left = node
def remove(self, num: int):
"""删除节点 - 递归实现"""
self._root = self._remove_recursive(self._root, num)
def _remove_recursive(self, node: TreeNode, num: int):
"""递归删除节点的辅助函数"""
if node is None:
return None
# 找到需要删除的节点
if num < node.val:
node.left = self._remove_recursive(node.left, num)
elif num > node.val:
node.right = self._remove_recursive(node.right, num)
else:
# 节点度为 0 或 1
if node.left is None:
return node.right
elif node.right is None:
return node.left
# 节点度为 2,找到右子树中序遍历的下一个节点(即最小值)
min_larger_node = self._find_min(node.right)
node.val = min_larger_node.val
# 删除右子树中的最小值节点
node.right = self._remove_recursive(node.right, min_larger_node.val)
return node
def _find_min(self, node: TreeNode):
"""找到子树中的最小节点"""
while node.left is not None:
node = node.left
return node
"""Driver Code"""
if __name__ == "__main__":
# 初始化二叉搜索树
bst = BinarySearchTree()
nums = [4, 2, 6, 1, 3, 5, 7]
for num in nums:
bst.insert(num)
# 删除节点
bst.remove(1) # 度为 0
bst.remove(2) # 度为 1
bst.remove(4) # 度为 28.1.4 中序遍历有序
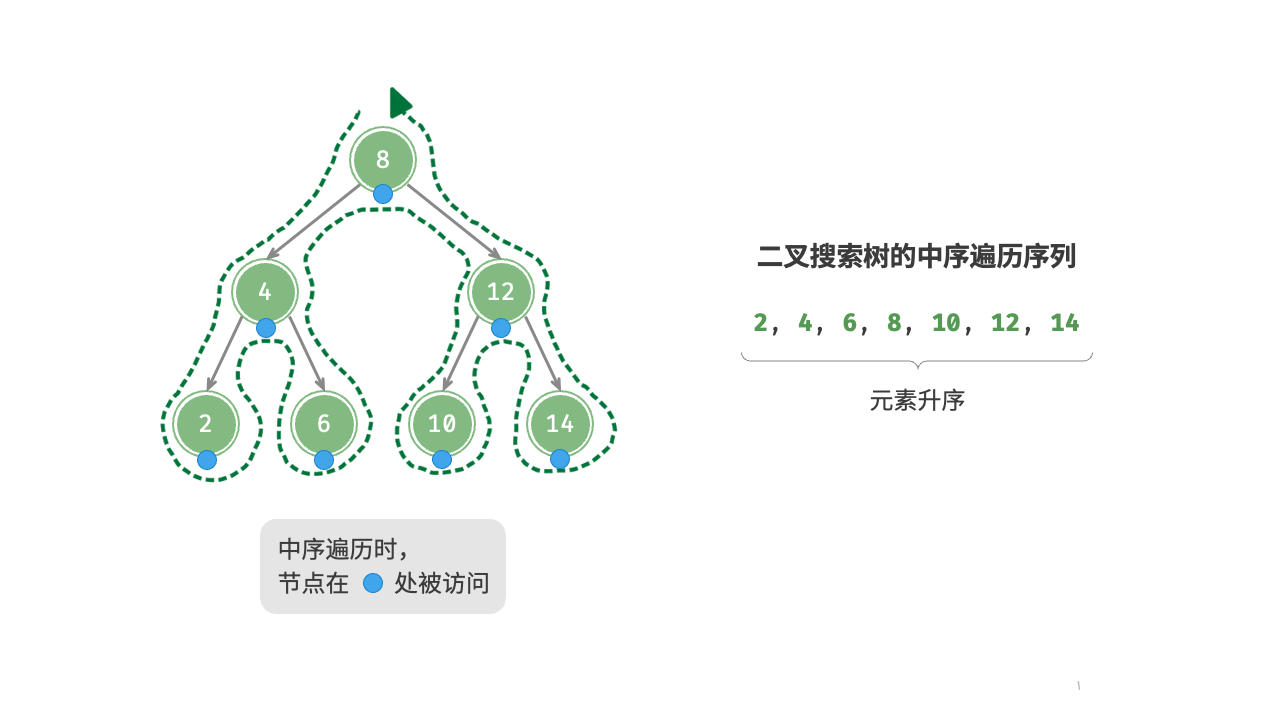
如图 7-22 所示,二叉树的中序遍历遵循“左 根 右”的遍历顺序,而二叉搜索树满足“左子节点 根节点 右子节点”的大小关系。
这意味着在二叉搜索树中进行中序遍历时,总是会优先遍历下一个最小节点,从而得出一个重要性质:二叉搜索树的中序遍历序列是升序的。
利用中序遍历升序的性质,我们在二叉搜索树中获取有序数据仅需 时间,无须进行额外的排序操作,非常高效。
8.2 二叉搜索树的效率
给定一组数据,我们考虑使用数组或二叉搜索树存储。观察表 7-2 ,二叉搜索树的各项操作的时间复杂度都是对数阶,具有稳定且高效的性能。只有在高频添加、低频查找删除数据的场景下,数组比二叉搜索树的效率更高。
表 7-2 数组与搜索树的效率对比
| 无序数组 | 二叉搜索树 | |
|---|---|---|
| 查找元素 | ||
| 插入元素 | ||
| 删除元素 |
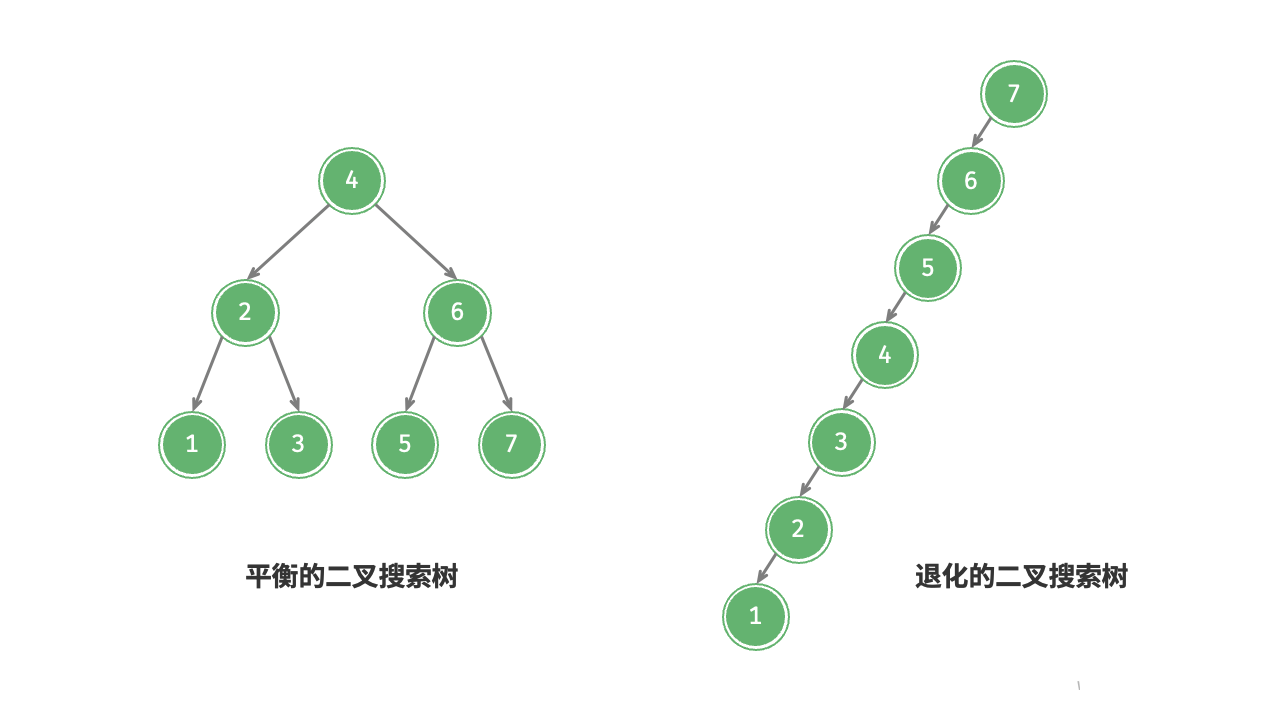
在理想情况下,二叉搜索树是“平衡”的,这样就可以在 轮循环内查找任意节点。
然而,如果我们在二叉搜索树中不断地插入和删除节点,可能导致二叉树退化为图 7-23 所示的链表,这时各种操作的时间复杂度也会退化为 。
8.3 二叉搜索树常见应用
- 用作系统中的多级索引,实现高效的查找、插入、删除操作。
- 作为某些搜索算法的底层数据结构。
- 用于存储数据流,以保持其有序状态。
9. AVL 树 *
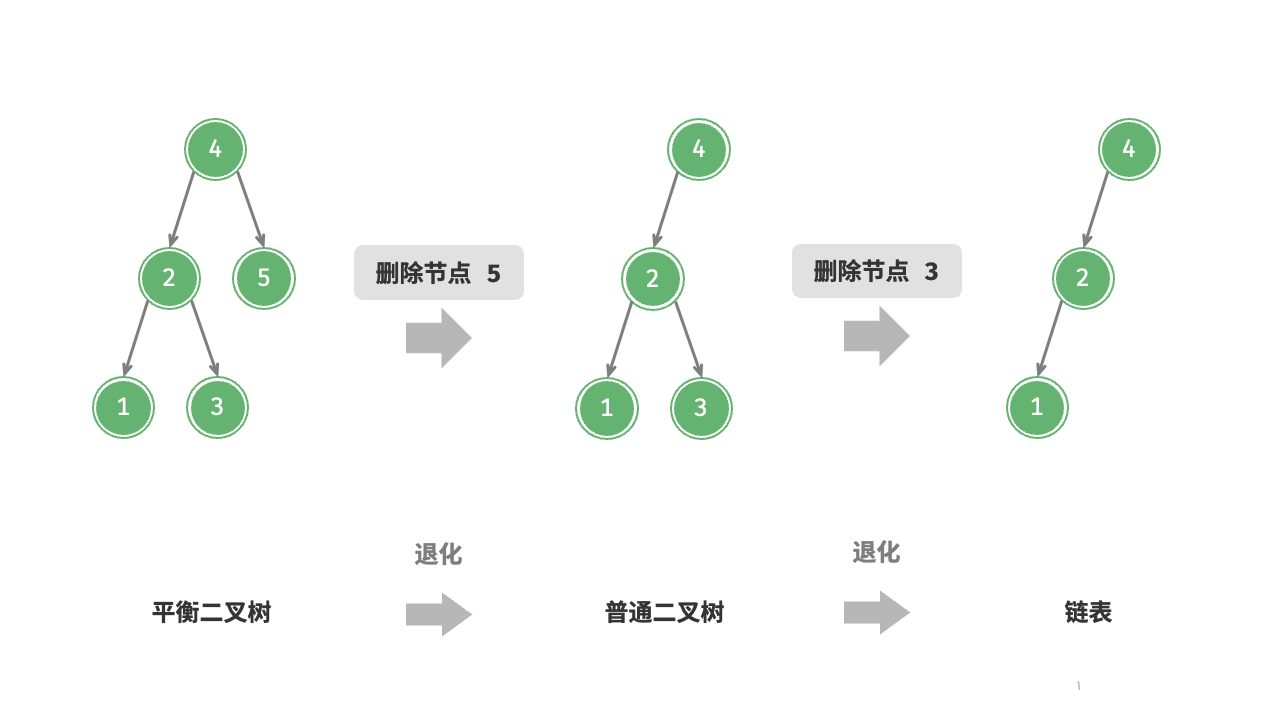
在“二叉搜索树”章节中我们提到,在多次插入和删除操作后,二叉搜索树可能退化为链表。在这种情况下,所有操作的时间复杂度将从 劣化为 。
如图 7-24 所示,经过两次删除节点操作,这棵二叉搜索树便会退化为链表。
Other
二叉树的时间复杂度为 ,这个常见于平衡二叉搜索树。我来用简单的方式为你解释一下。
- 什么是二叉树?
二叉树是一个树形结构,其中每个节点最多有两个子节点:一个左子节点和一个右子节点。一个常见的例子是二叉搜索树,它的性质是:对于每个节点,左子树的所有节点值都小于这个节点的值,右子树的所有节点值都大于这个节点的值。
- 树的高度是什么?
树的高度指的是从根节点到最深的叶子节点的路径长度。比如:
- 如果一个二叉树只有一个节点,树的高度是 0。
- 如果一个二叉树有两个节点,根节点和一个叶子节点,那么树的高度是 1。
在一个理想的平衡二叉树中,如果有 n 个节点,那么树的高度大约是 ,这是因为每一层的节点数是前一层的两倍。
- 为什么是 ?
假设你有一棵平衡的二叉树,并且它的高度为 h,那么这棵树最多可以容纳的节点数是 个。也就是说:
- 高度为 1 时,最多有 1 个节点()
- 高度为 2 时,最多有 3 个节点()
- 高度为 3 时,最多有 7 个节点()
可以看到,随着树的高度增加,节点的数量呈指数级增长。
要插入、查找或删除一个节点时,你需要从树的根开始,逐层往下找到合适的位置。每向下一层,树的节点数就会减半。换句话说,你在查找的过程中,每一步都缩小了一半的范围。因此,这种操作的时间复杂度是与树的高度成正比的。
对于一个有 n 个节点的平衡二叉树,树的高度大约是 ,所以插入、查找或删除操作的时间复杂度也是 。
- 总结
- 二叉树操作的时间复杂度通常和树的高度有关。
- 对于一个有
n个节点的平衡二叉树,树的高度大约是 。 - 查找、插入、删除操作的复杂度都与树的高度相关,所以在平衡二叉树中的这些操作通常为 。
在二叉树的时间复杂度为 中,底数是 2。
为什么底数是 2?
这是因为在每一层,平衡二叉树的节点数会 翻倍。具体来说:
- 在树的第 0 层(根节点),有 1 个节点。
- 在树的第 1 层,有 2 个节点。
- 在树的第 2 层,有 4 个节点。
- 在树的第 3 层,有 8 个节点。
因此,树的每一层的节点数以 的形式增长, 是层数(高度)。这个增长模式导致树的高度与节点总数之间的关系是以 2 为底的对数关系。所以,复杂度表示为 ,其中底数是 2。
不过,计算机科学中的对数复杂度通常忽略底数,因为不同底数的对数之间的差别只是一个常数倍,并不会影响大规模情况下的渐进复杂度。因此,常常简写为 ,不具体说明底数。但从数学上讲,这里的底数是 2。
公众号:AI悦创【二维码】

AI悦创·编程一对一
AI悦创·推出辅导班啦,包括「Python 语言辅导班、C++ 辅导班、java 辅导班、算法/数据结构辅导班、少儿编程、pygame 游戏开发、Web、Linux」,全部都是一对一教学:一对一辅导 + 一对一答疑 + 布置作业 + 项目实践等。当然,还有线下线上摄影课程、Photoshop、Premiere 一对一教学、QQ、微信在线,随时响应!微信:Jiabcdefh
C++ 信息奥赛题解,长期更新!长期招收一对一中小学信息奥赛集训,莆田、厦门地区有机会线下上门,其他地区线上。微信:Jiabcdefh
方法一:QQ
方法二:微信:Jiabcdefh

更新日志
1c35a-于aed17-于a79b0-于d0112-于a3db3-于7fbc2-于96d4c-于37b56-于a4ae2-于ceb85-于0c2c8-于af796-于45f9e-于d3187-于a1df3-于64b86-于40b1b-于abcbb-于ffb04-于7c20f-于86740-于d22b5-于5d707-于44952-于021b4-于01c20-于81eaf-于a35f4-于edb3c-于4b115-于d12b0-于76c91-于55ad4-于09013-于68b0d-于169dc-于0c00e-于a28ad-于d23dc-于a5fb1-于ce59d-于26637-于13271-于70f72-于f937b-于4fd5e-于01745-于27023-于a1f1e-于cbb3a-于610fe-于f08aa-于76989-于86c50-于027da-于