Python 滑动窗口算法

1. 滑动窗口的基本概念

滑动窗口通常用来减少不必要的计算，提高效率。 基本的思想是创建一个窗口，这个窗口可以覆盖数组的一部分，然后根据需要向前滑动。在滑动过程中，你可以更新一些信息，而不是重新计算整个窗口的信息。

滑动窗口主要用来处理连续问题。比如题目求解“连续子串 xxxx”，“连续子数组 xxxx”，就应该可以想到滑动窗口。能不能解决另说，但是这种敏感性还是要有的。

从类型上说主要有：

• 固定窗口大小
• 窗口大小不固定，求解最大的满足条件的窗口
• 窗口大小不固定，求解最小的满足条件的窗口

后面两种我们统称为可变窗口。当然不管是哪种类型基本的思路都是一样的，不一样的仅仅是代码细节。

2. 固定窗口大小

对于固定窗口，我们只需要固定初始化左右指针 l 和 r，分别表示窗口的左右顶点，并且保证：

1. l 初始化为 0
2. 初始化 r，使得 r-l+1 等于窗口大小
3. 同时移动 l 和 r
4. 判断窗口内的连续元素是否满足题目限定的条件
   1. 如果满足，再判断是否需要更新最优解，如果需要则更新最优解
   2. 如果不满足，则继续

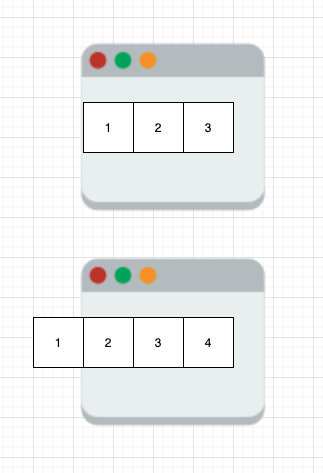
2.1 基本组成

• 窗口大小：窗口的大小固定或变动，取决于问题的需求。
• 窗口状态：可以是窗口内的元素和、最大值、最小值等。
• 左右指针：用来表示窗口的边界，通常用两个变量 left 和 right 表示。

2.2 操作流程

• 初始化窗口：设置窗口的初始位置和大小。
• 窗口滑动：根据问题的需求移动左右指针。
• 更新状态：在窗口滑动的同时更新需要维护的状态。
• 记录结果：根据问题需要记录窗口的状态或最终结果。

2.3 小试牛刀：找到数组中大小为 k 的连续子数组的最大总和

我们用一个简单的例子来介绍滑动窗口的概念。比如说，我们有一个数组 [1, 3, -1, -3, 5, 3, 6, 7] 和一个数字 k = 3，我们的目标是找出所有大小为 k 的连续子数组的最大总和。

这个问题是滑动窗口技术在数组中的典型应用。所谓滑动窗口，就是在数组或列表的一段固定大小的连续元素区间中滑动，以进行一些特定的运算。在这个例子中，我们需要找到连续的 k 个元素的最大总和。

首先，我们来定义问题需求：

• 给定一个整数数组和一个数字 k。
• 找出所有大小为 k 的连续子数组的最大总和。

2.4 解题步骤

1. 初始化：首先，定义一个变量来存储当前窗口的总和（称为 current_sum），以及一个变量来存储迄今为止找到的最大总和（称为 max_sum）。

2. 首个窗口的总和：计算数组中前 k 个元素的总和，这将是第一个窗口的总和。

3. 滑动窗口：遍历数组，从索引 k 到 数组长度-1。每向右滑动窗口一步：

   1. 从 current_sum 中减去窗口最左边的元素。
   2. 加上新进入窗口的元素（即当前索引所指的元素）。
   3. 更新 max_sum 为 current_sum 和 max_sum 中的较大值。

4. 输出结果：遍历完成后，max_sum 将是所有大小为 k 的连续子数组中的最大总和。

2.5 示例代码

假设我们有数组 arr = [1, 3, -1, -3, 5, 3, 6, 7] 和 k = 3，下面是用 Python 实现的代码：

def find_max_sum_of_k_subarray(arr, k):
    n = len(arr)
    if n < k:
        return 0  # 如果数组长度小于 k，则无法形成大小为 k 的子数组

    # 计算第一个窗口的总和
    current_sum = sum(arr[:k])
    max_sum = current_sum

    # 开始滑动窗口
    for i in range(k, n):
        current_sum += arr[i] - arr[i - k]  # 加入新元素，移除旧元素
        max_sum = max(max_sum, current_sum)  # 更新最大总和

    return max_sum

# 测试
arr = [1, 3, -1, -3, 5, 3, 6, 7]
k = 3
print(find_max_sum_of_k_subarray(arr, k))  # 输出应为 16

这段代码首先处理了一些边界情况（例如数组长度小于 k），然后计算了第一个窗口的总和，并通过滑动窗口的方式更新了当前窗口的总和和迄今为止的最大总和。最终，返回了最大的总和。这种方法的时间复杂度为 $O(n)$，其中 n 是数组的长度，因为每个元素只被访问了两次（一次加入窗口，一次离开窗口）。

2.6 部分思路「下一组数据」

在滑动窗口算法中，更新当前窗口总和的这一步可以拆解为两个部分来理解：

1. 移除旧元素：

   • 首先，我们需要从当前窗口的总和中减去窗口最左侧的元素，也就是即将离开窗口的元素。这一步是为了让窗口向右移动一位，因此需要排除旧窗口中最前面的那个元素。
   • 代码表达为：current_sum -= arr[i - k]
   • 这里的 i - k 表示的是在当前索引 i 的位置向左 k 个元素的位置，即窗口的最左侧元素。

2. 添加新元素：

   • 然后，向当前总和中添加新的元素，也就是新窗口中最右侧的元素，这个元素在数组中的位置是 i。
   • 代码表达为：current_sum += arr[i]
   • 这里的 i 是当前遍历到的数组元素的索引，也是新进入窗口的元素的索引。

将这两步结合起来，你就得到了 current_sum += arr[i] - arr[i - k] 这一行代码的完整意义：更新窗口内元素的总和，以反映窗口向右移动一位后的新状态。通过这种方式，你每次都能得到新窗口中所有元素的总和，而无需重新对窗口内的所有元素求和，从而提高了算法的效率。

这种方法保证了算法的时间复杂度为 $O(n)$，因为每个元素只被加入和移除一次。这也是滑动窗口技术特别适用于处理大数据流或需要快速响应的场景的原因之一。

2.7 编程题

2.7.1 题目1：最大平均值子数组

2.7.1.1 问题描述：

给定一个由整数组成的数组和一个整数 k，找到该数组中大小为 k 的连续子数组的最大平均值，并返回这个最大平均值。

2.7.1.2 示例：

• 输入: [1,12,-5,-6,50,3], k = 4
• 输出: 12.75
• 解释: 最大平均值 12.75 是从第二个到第五个元素的平均值 (12 - 5 - 6 + 50)/4 = 12.75。

2.7.1.3 解题思路：

使用固定大小为 k 的滑动窗口来遍历数组，记录每个窗口的元素总和，并计算其平均值，更新最大平均值。

2.7.2 题目2：包含最多水的容器

2.7.2.1 问题描述：

给定一个正整数数组 height，其中 height[i] 表示在坐标 (i, 0) 处的一个点的高度，你需要找到两条线，它们与 x 轴共同构成一个容器，使得容器可以包含最多的水。

2.7.2.2 示例：

• 输入: [1,8,6,2,5,4,8,3,7]
• 输出: 49
• 解释: 选择索引 1 和 8 的线，这时高度为 7（较小的一边），长度为 7，所得到的容器可以装 7 * 7 = 49 单位的水。

2.7.2.3 解题思路：

虽然这个问题看起来和滑动窗口技术不太相关，实际上可以用双指针的方法模拟滑动窗口。从数组的两端开始，向中间收缩，每次移动较短的一边的指针，计算并更新最大水容量。

2.7.3 题目3：字符的最短距离

2.7.3.1 问题描述：

给你一个字符串 s 和一个字符 c，返回一个整数数组 answer，其中 answer.length == s.length，answer[i] 是 s[i] 与 s 中所有 c 字符之间的最短距离。

2.7.3.2 示例：

• 输入: s = "loveleetcode", c = 'e'
• 输出: [3, 2, 1, 0, 1, 0, 0, 1, 2, 2, 1, 0]
• 解释: 字符 e 出现在 s 中的索引 3, 5, 6, 11，输出数组是每个字符到最近的 e 的距离。

2.7.3.3 解题思路：

可以通过两次遍历字符串来解决这个问题。第一次从左到右，计算每个字符到左侧最近的 c 的距离。第二次从右到左，计算每个字符到右侧最近的 c 的距离，并更新为最小距离。

这些题目都可以通过固定滑动窗口或双指针技术来解决，非常适合锻炼对这种技术的理解和应用。

欢迎关注我公众号：AI悦创，有更多更好玩的等你发现！

公众号：AI悦创【二维码】