Homework 5
Instructions: This homework is to be submitted on GradeScope as a single pdf (not in parts) by 11:59 pm on the due date. You may either type your solutions in a word processor and print to a pdf, or write them by hand and submit a scanned copy. Do write and submit your answers as if they were a professional report. There will be point deductions if the submission isn’t neat (is disordered, difficult to read, scanned upside down, etc...).
Begin by reviewing your class notes, the slides, and the textbook. Then do the exercises below. Show your work. An unjustified answer may receive little or no credit.
Schedule: You can do all problems right now, except for problems 7, 9, 10 that require Tuesday’s class.
Read: 1.3 (for Tuesday) and 1.4 (for Friday)
- [4 Points] Use the listing method to describe the language that is accepted by the nondeterministic automaton

详情
语言 接受的字符串为: 即,L 包含所有零个或多个 后跟一个 的字符串,以及空 。
根据图片中的非确定性有限自动机(NFA),一开始传入的数据是 ε(空串)。从图中可以看到,最左边的初始状态有一个箭头指向下一状态,箭头标记为 ε,表示在无需输入任何字符(即输入空串 ε)的情况下,自动机可以自由地移动到下一个状态。
因此,最开始传入的数据是 ε,即空串。
根据状态图的结构,任意数量的 也能够被接受,因为有一条从最后一个状态通过 -转移直接回到初始状态。这意味着,除了形如 ( a^n b ) 的字符串外,形如 (即仅包含任意数量的 )的字符串也可以被接受。
因此,最终的语言 应该包含以下形式的字符串:
- 空串 。
- 任意数量的 ,即 (n 为非负整数)。
- 任意数量的 ( a ) 后跟一个 ,即 (n 为非负整数)。
最终答案:
语言 接受的字符串为:
这意味着, 包含了任意数量的 和至多一个 的所有字符串。
- [6 Points] The nondeterministic finite automaton below is defined over the alphabet . Formally describe it by specifying each component of the quintuple .
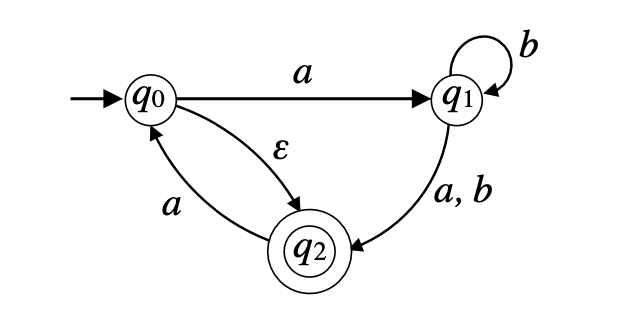
详情
- 状态集合 Q:
该自动机有三个状态 , 和
- 字符串表
字母表由 和 组成。
- 转换函数 : 转换函数定义如下:
- (状态 接受 a 后可以转移到 或 )
- (状态 接受 空转后可以转移到 )
- (状态 接受 后转移到 )
- (状态 接受 后保持在 ))
- (状态 接受 后保持在 )
- (状态 接受 后保持在 )
- 起始状态 :
- 终止状态集合 :
终止状态为 。
总结:
- [5 Points] NFAs. Let and let
For example, because there are exactly 6 characters between the third and the last , but . Draw the state-diagram of a NFA that accepts .
详情
要设计一个非确定性有限自动机(NFA),它接受语言 ( L ),其中 ,即字符串中至少有两个字符 'a',且它们之间有恰好 6 个字符。
NFA 设计:
- 状态 :初始状态,等待第一个 'a' 出现。
- 状态 :读到了第一个 'a',开始计数接下来出现的字符。
- 状态 :依次表示在第一个 'a' 之后读入的第1至第6个字符,无论是 'a' 还是 'b'。
- 状态 :当读到第6个字符后,自动机期待另一个 'a'。
- 状态 :接受状态,表示读到第二个 'a',且它与第一个 'a' 之间恰好有 6 个字符。
状态集合 :
- 状态:
- 初始状态:
- 接受状态:
字母表:
字母表包含 a 和 b。
转换函数
从 :
读到 时,转移到 。
读到 或 时,保持在 。(因为我们可以在任何位置开始新的匹配)
从 到 :
- 对于每个状态 ( 到 ),读到任意字符 或 时,转移到下一个状态 。
从 :
读到 时,转移到接受状态 。
读到 或 时,保持在 。(表示等待下一个 )
从接受状态 :
- 读到任意字符 或 时,保持在 $q_f $。
状态图示意:
(q0) --a--> (q1) --a,b--> (q2) --a,b--> (q3) --a,b--> (q4) --a,b--> (q5) --a,b--> (q6) --a,b--> (q7) --a--> [qf] ^ | |------------------------------------------| 输入 a 或 b,循环回 q0状态转移表:
| 当前状态 | 输入字符 | 下一状态 |
|---|---|---|
- [10 Points] NFAs. Let and let
Draw the state-diagram of a NFA that accepts L.
详情
NFA 的状态设计:
- 初始状态 :从这里开始读取字符。
- 中间状态 (多个状态用于处理读取的字符):
- 每读一个字符,继续前进。
- 分支状态 :非确定性地猜测当前字符是否是最后一个字符。
- 检查状态 :一旦猜测了某个字符是最后一个字符,就需要检查它是否出现在之前的输入中。
- 接受状态 :如果最后一个字符没有在之前出现过,自动机接受该字符串。
- 拒绝状态 :如果最后一个字符在之前出现过,则转到拒绝状态。
(q0) --[b,c,d]--> (q1) --[b,c,d]--> (q1)
| |
[a] [a]
| |
↓ ↓
(q_fail) (q_accept) 输入 a
+---------> (q_fail)
|
(q0) ---|
|
+--- 输入 b,c,d ---> (q1)
|
| 输入 x ∈ {a,b,c,d}
v
+-----------+
| |
| 非确定性 |
| |
+-----------+
|
+--------------------------------+
| |
v v
(q_accept_x) [x 未出现过且为最后一个字符] (q_fail)
[x 已出现过]
|
| [否则]
v
(q1) [保持在 q1]- [10 Points] Give the state diagram of a NFA with at most six states for the language
详情
'a' 'a'
+--------+ +--------+
| v v |
+--+--+ +---+---+ +---+---+
| q0 |--'a'->| q1 |--'a'->| q0 |
|(初始,接)| | | |
+--+--+ +---+---+ +---+---+
| | |
'b' 'b' 'b'
v v v
+---+---+ +-----------+
| q2 |<----------------+
+---+---+ 'a' 或 'b' 转移
| |
'b' 'a'
v |
+---+---+
| q3 | (接受状态)
+---+---+
|
'b'
v
+---+---+
| q4 | (死状态)
+-------+(q0) --a--> (q1) --a--> (q2) --a--> (q1) (处理偶数个 a 的路径)
| |
b b
v v
(q4) --b--> (q5) (q2) (处理恰好两个 b 的路径)- [15 Points] Let and consider the languages
and .
(a) Draw the state diagram of a DFA for .
(b) Draw the state diagram of a DFA for .
(c) Draw the state diagram of a NFA for .
详情
a.
(q0) --0,1--> (q1) --0,1--> (q2) --0,1--> (q3) --0,1--> (q4) --0,1--> (q5)
|
v
(qrej)b.
(q0) --0--> (qrej)
| |
1 0,1
| |
(q1) --0,1--> (q0)c.
(q0) --0,1--> (q1) --0,1--> (q2) --0,1--> (q3) --0,1--> (q4) --0,1--> (q5)
|
v
(qrej)
|
(q0_L2) --0--> (qrej_L2)
|
1
|
(q1_L2) --0,1--> (q0_L2)- [8 Points] Let .
(a) Give the state diagram of a DFA for .
(b) Use the method from Lecture 10 to construct the state diagram of a NFA for .
详情
q0 --0--> q1 --0--> q3 (接受状态)
| | |
1| 1| 1|
v v v
q2 --0--> q4 (接受状态)
| |
1| 1|
v v
q5 q5
q3 --0--> q3
|
1|
v
q4
q4 --0--> q4
|
1|
v
q5
q2 --1--> q5(q0) --0--> (q1) --0--> (q2) --0--> (q2)
| | |
1 1 |
v v |
(q3) (q3) ε
^ |
|---|- [11 Points] Use the subset method from Lecture 9 to convert the following nondeterministic finite automata to equivalent deterministic finite automata.
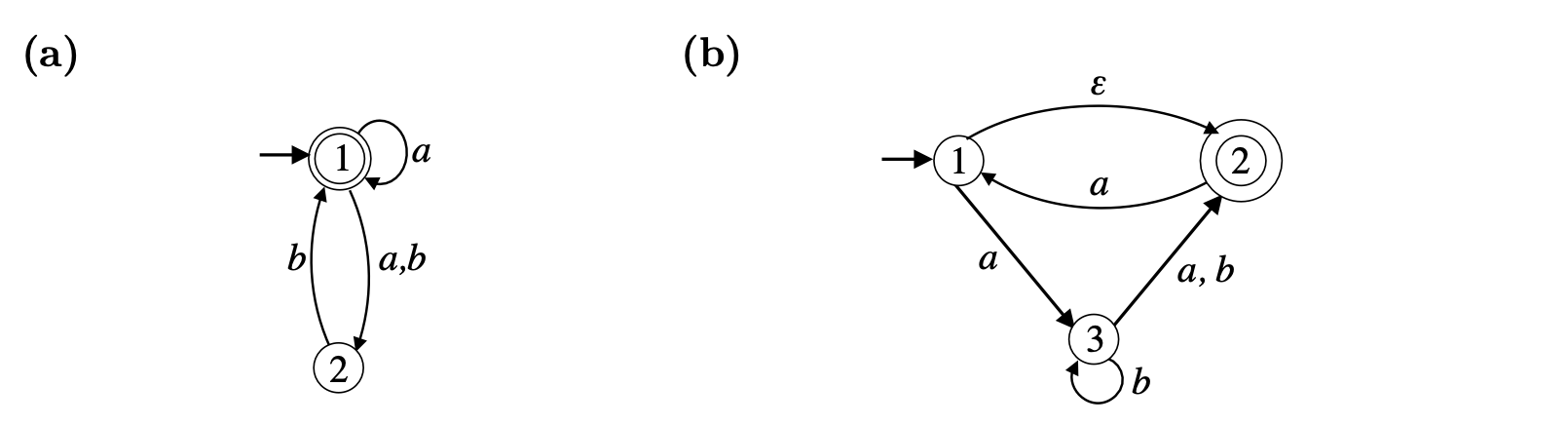
详情
(a) NFA 转换为 DFA
图 (a) 的 NFA 概述:
- 状态集合:
- 字母表:
- 初始状态:1
- 接受状态:1
- 转换规则:
- 从状态 1 通过 回到状态 1。
- 从状态 1 通过 转到状态 2。
- 从状态 2 通过 或 回到状态 2。
子集构造法步骤:
初始状态的 ε-闭包:
- 初始状态是 (1),因为没有 ε-转换,初始状态的 ε-闭包为 。
- 因此,DFA 的初始状态为 。
从状态 的转换:
- 对输入 :从状态 1 经过 转换回自身,即 。
- 对输入 :从状态 1 经过 转换到状态 2,即 。
从状态 的转换:
- 对输入 :从状态 2 经过 回到状态 2,即 。
- 对输入 :从状态 2 经过 (b) 也回到状态 2,即 。
接受状态:
- NFA 的接受状态是 ,因此 DFA 中包含状态 的集合也是接受状态。
- DFA 的接受状态为 。
最终的 DFA 状态转换表:
状态 输入 输入 DFA 状态图:
(q1) --a--> (q1)
| |
b b
v v
(q2) <------ (q2)- 是初始状态也是接受状态, 不是接受状态。
(b) NFA 转换为 DFA
图 (b) 的 NFA 概述:
- 状态集合:
- 字母表:
- 初始状态:1
- 接受状态:2
- 转换规则:
- 从状态 1 通过 ε 转换到状态 2。
- 从状态 1 通过 转换到状态 3。
- 从状态 2 通过 转换到状态 3,并通过 ε 转换回状态 1。
- 从状态 3 通过 返回自身。
子集构造法步骤:
初始状态的 ε-闭包:
- 从状态 可以通过 ε 转换到状态 ,因此 ε-闭包为 。
- 因此,DFA 的初始状态为 。
从状态 的转换:
- 对输入 :从状态 1 和 2 都可以通过 转到状态 3,因此 。
- 对输入 :状态 1 和 2 没有经过 的转换,因此 。
从状态 的转换:
- 对输入 :状态 3 没有经过 的转换,因此 。
- 对输入 :状态 3 通过 转换回自身,因此 。
从状态 的转换:
- 从空状态 对任意输入都没有转换,因此它会保持在 状态。
接受状态:
- NFA 的接受状态是 ,因此任何包含 的集合是 DFA 的接受状态。
- DFA 的接受状态为 。
最终的 DFA 状态转换表:
状态 输入 输入 DFA 状态图:
(q0) --a--> (q3)
| |
b b
v v
(qrej) <--- (q3)- () 是初始状态也是接受状态。
- 是状态 3,对 有自环。
- 是空状态,不接受任何输入。
- [18 Points] For each of the following statements, state whether it is true or false. Explain.
(a)
(b)
(c)
(d)
(e)
(f)
详情
(a) 真。
解释:字符串 baa 可以分解为:
- 第一个
a^*:空('') - 第一个
b^*:b - 第二个
a^*:aa - 第二个
b^*:空('')
因此,baa 属于正则表达式 a^*b^*a^*b^*。
(b) 假。
解释:a^* \cup b^* 表示只包含 a 或只包含 b 的所有字符串(包括空串)。而 (a \cup b)^* 表示由 a 和 b 构成的任意字符串(包括空串)。例如,字符串 ab 属于 (a \cup b)^*,但不属于 a^* \cup b^*。因此,两者不相等。
(c) 真 false
解释:(a^*b^*)^* 表示由零个或多个形如 a^*b^* 的字符串连接而成的字符串集。由于每个 a^*b^* 可以生成任何由 a 和 b 构成的字符串(通过选择适当数量的 a 和 b),因此 (a^*b^*)^* 等价于 (a \cup b)^*。
(d) 真。
解释:b^*a^* 和 a^*b^* 的交集只包含仅由 a 构成的字符串、仅由 b 构成的字符串和空串,即 a^* \cup b^*。因为其他字符串的字符顺序无法同时满足这两个正则表达式的要求。
(e) 假。
解释:虽然 a^*b^* 和 c^*d^* 使用了不同的字符集,但空串属于这两个正则表达式的语言。因此,它们的交集至少包含空串,不是空集。
(f) 假。
解释:(a(cd)^*b)^* 中的基本单元是以 a 开头、零个或多个 cd、以 b 结尾的字符串的重复。abcd 无法由这种结构的字符串通过连接得到,因此 abcd 不属于该正则表达式描述的语言。
- [8 Points] Let . Write regular expressions for the languages
(a) All strings in with no more than three 's.
(b) All strings in with a number of 's divisible by 3.
详情
(a) 正则表达式:
(b)* (a (b)*)? (a (b)*)? (a (b)*)?解释:字符串可以包含0到3个a,每个a前后可以有任意多个b。
(b) 正则表达式:
((b)* a (b)* a (b)* a (b)*)* (b)*解释:每组包含三个a,每个a前后可以有任意多个b,整个模式可以重复任意次(包括0次),最后可能再跟任意多个b。
- [5 Points] Tint. (Submission is separate from the other problems.) Let
A string of symbols from defines two rows of 0s and 1s. Consider each row to be a binary number and let
For example,
because, as binary numbers, 0011 < 0100.
Construct a finite automaton that accepts ( D ). Note that, due to the linearity of symbols in tint, the columns above have to be represented by strings of length 2. That is, . And "00 01 10 10" because, as binary numbers, 0011 < 0100.
详情
- [0 Point] Do not submit. Exercise 1.7(af) page 84. The solution is in the book page 96, this is for practice only.
公众号:AI悦创【二维码】

AI悦创·编程一对一
AI悦创·推出辅导班啦,包括「Python 语言辅导班、C++ 辅导班、java 辅导班、算法/数据结构辅导班、少儿编程、pygame 游戏开发、Web、Linux」,全部都是一对一教学:一对一辅导 + 一对一答疑 + 布置作业 + 项目实践等。当然,还有线下线上摄影课程、Photoshop、Premiere 一对一教学、QQ、微信在线,随时响应!微信:Jiabcdefh
C++ 信息奥赛题解,长期更新!长期招收一对一中小学信息奥赛集训,莆田、厦门地区有机会线下上门,其他地区线上。微信:Jiabcdefh
方法一:QQ
方法二:微信:Jiabcdefh

更新日志
1c35a-于aed17-于2383e-于235bc-于64e71-于44952-于edb3c-于